Инструкция
1
Для нахождения внутреннего угла треугольника вспомните теорему о сумме углов треугольника.
Теорема: сумма углов треугольника равна 180°.
Из этой теоремы выделите пять следствий, которые могут помочь в расчете внутреннего угла.
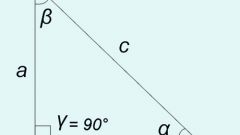
1. Сумма острых углов прямоугольного треугольника равна 90°.
2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
3. В равностороннем треугольнике каждый угол равен 60°.
4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
5. Внешний угол треугольника равен сумме двух внутренних углов.
Пример 1:
Найти углы треугольника АВС, зная, что угол С на 15° больше, а угол И на 30° меньше угла А.
Решение:
Обозначьте градусную меру угла А через Х, тогда градусная мера угла С равна Х+15°, а угол В равен Х-30°. Так как сумма внутренних углов треугольника равна 180°, то вы получите уравнение:
Х+(Х+15)+(Х-30)=180
Решая его, вы найдете Х=65°. Таким образом угол А равен 65°, угол В равен 35°, угол С равен 80°.
Теорема: сумма углов треугольника равна 180°.
Из этой теоремы выделите пять следствий, которые могут помочь в расчете внутреннего угла.
1. Сумма острых углов прямоугольного треугольника равна 90°.
2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
3. В равностороннем треугольнике каждый угол равен 60°.
4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
5. Внешний угол треугольника равен сумме двух внутренних углов.
Пример 1:
Найти углы треугольника АВС, зная, что угол С на 15° больше, а угол И на 30° меньше угла А.
Решение:
Обозначьте градусную меру угла А через Х, тогда градусная мера угла С равна Х+15°, а угол В равен Х-30°. Так как сумма внутренних углов треугольника равна 180°, то вы получите уравнение:
Х+(Х+15)+(Х-30)=180
Решая его, вы найдете Х=65°. Таким образом угол А равен 65°, угол В равен 35°, угол С равен 80°.
2
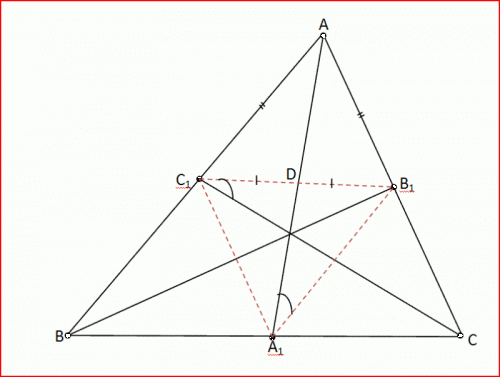
Поработайте с биссектрисой угла. В треугольнике АВС угол А равен 60°, угол В равен 80°. Биссектриса АD этого треугольника отсекает от него треугольник АСD. Попробуйте найти углы этого треугольника. Постройте график для наглядности.
Угол DAB равен 30°, так как AD – биссектриса угла А, угол ADC равен 30°+80°=110° как внешний угол треугольника ABD (следствие 5), угол С равен 180°-(110°+30°)=40° по теореме о сумме углов треугольника ACD.
Угол DAB равен 30°, так как AD – биссектриса угла А, угол ADC равен 30°+80°=110° как внешний угол треугольника ABD (следствие 5), угол С равен 180°-(110°+30°)=40° по теореме о сумме углов треугольника ACD.
3
Еще для нахождения внутреннего угла вы можете использовать равенство треугольников:
Теорема 1: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
На основе Теоремы 1 устанавливается Теорема 2.
Теорема 2: Сумма любых двух внутренних углов треугольника меньше 180°.
Из предыдущей теоремы вытекает Теорема 3.
Теорема 3: Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Также для вычисления внутреннего угла треугольника можно использовать теорему косинусов, но только в том случае, если известны все три стороны.
Теорема 1: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
На основе Теоремы 1 устанавливается Теорема 2.
Теорема 2: Сумма любых двух внутренних углов треугольника меньше 180°.
Из предыдущей теоремы вытекает Теорема 3.
Теорема 3: Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Также для вычисления внутреннего угла треугольника можно использовать теорему косинусов, но только в том случае, если известны все три стороны.
4
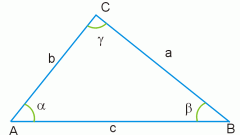
Вспомните теорему косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a2=b2+c2-2bc cos A
или
b2=a2+c2- 2ac cos B
или
с2=a2+b2-2ab cos C
a2=b2+c2-2bc cos A
или
b2=a2+c2- 2ac cos B
или
с2=a2+b2-2ab cos C
Источники:
- вычислить внутренние углы треугольника