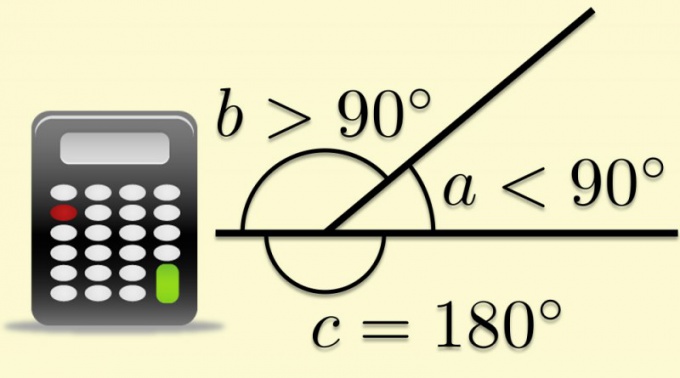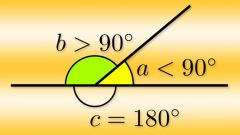Как найти косинус внешнего угла

Любой плоский угол можно достроить до развернутого, если продлить за вершину одну из его сторон. При этом другая сторона будет делить развернутый угол на два. Угол, образуемый второй стороной и продолжением первой, называется смежным, а когда речь идет о многоугольниках, его называют еще и внешним. Тот факт, что сумма внешнего и внутреннего углов по определению равна величине развернутого угла, позволяет вычислять тригонометрические функции по известным соотношениям параметров многоугольников.

Инструкция

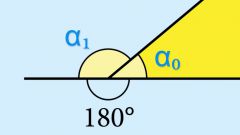
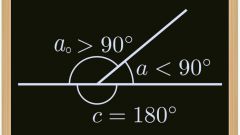
1. Зная результат вычисления косинуса внутреннего угла (α) вы будете знать модуль косинуса внешнего (α₀). Единственная операция, которую вам нужно произвести с этой величиной - изменить ее знак, то есть умножить на -1: cos(α₀) = -1*cos(α).
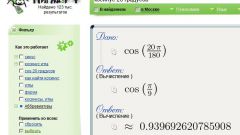
2. Если известна величина внутреннего угла (α), для вычисления косинуса внешнего (α₀) можно использовать способ, описанный в предыдущем шаге - найти его косинус, а затем поменять знак. Но можно сделать и по-другому - сразу вычислить косинус внешнего угла, отняв для этого величину внутреннего от 180°: cos(α₀) = cos(180°-α). Если величина внутреннего угла приведена в радианах, формулу нужно преобразовать к такому виду: cos(α₀) = cos(π-α).
3. В правильном многоугольнике для вычисления величины внешнего угла (α₀) не нужно знать никаких параметров, кроме количества вершин (n) этой фигуры. На это число разделите 360° и найдите косинус полученного числа: cos(α₀) = cos(360°/n). Для вычислений в радианах на число вершин надо делить удвоенное число Пи, а формула должна приобрести такой вид: cos(α₀) = cos(2*π/n).
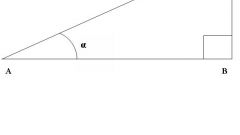
4. В прямоугольном треугольнике косинус внешнего угла при вершине, лежащей напротив гипотенузы, всегда равен нулю. Для двух других вершин эту величину можно рассчитать, зная длины гипотенузы (c) и катета (a), которые образуют эту вершину. Никаких тригонометрических функций при этом вычислять не требуется, просто разделите длину меньшей стороны на длину большей и поменяйте знак результата: cos(α₀) = -a/c.
5. Если известны длины двух катетов (a и b), тоже можно обойтись в расчетах без тригонометрических функций, но формула будет несколько сложней. Дробь, в знаменателе которой стоит длина стороны, примыкающей к вершине внешнего угла, а в числителе - длина другого катета, определяет тангенс внутреннего угла. Зная тангенс можно вычислить косинус внутреннего угла: √(1/(1+a²/b²). Этим выражением замените косинус в правой части формулы из первого шага: cos(α₀) = -1*√(1/(1+a²/b²).