Вам понадобится
  • - калькулятор;
  • - таблицы Брадиса;
  • - понятие теоремы Пифагора;
  • - тригонометрические тождества;
  • - линейка.
Инструкция
1
Измерьте или посчитайте угол, косинус которого нужно вычислить. Переключите инженерный калькулятор на вычисления в градусах, наберите это значение на его экране и нажатием кнопки вычислите косинус. Если такого калькулятора нет, найдите значение угла в соответствующем разделе таблиц Брадиса и найдите его косинус.
2
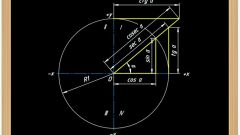
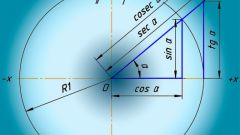
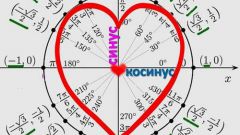
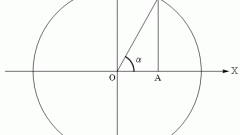
Вычислите косинус угла, который представляет собой поворот радиуса окружности с центром в начале координат относительно оси абсцисс. Для этого найдите абсциссу точки пересечения радиуса, ограничивающего угол с окружностью, которая и будет равна косинусу данного угла. Если окружность не единичная, поделите полученную абсциссу на значение радиуса.
3
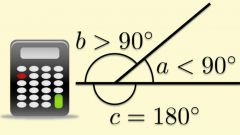
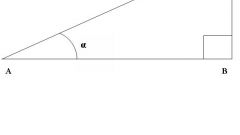
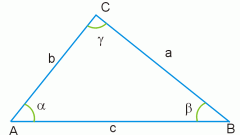
Найдите значение косинуса острого угла в прямоугольном треугольнике. Определите, какие из его сторон являются катетами (угол между ними равен 90˚). Третья сторона будет гипотенузой. Чтобы найти косинус острого угла, измерьте длину прилежащего к нему катета и длину гипотенузы, используя для этого линейку, или найдите неизвестную сторону по двум известным, используя теорему Пифагора. Косинус острого угла будет равен отношению прилежащего катета к гипотенузе. Например, если длина прилежащего катета равна 5 см, а длина гипотенузы составляет 10 см, то косинус этого угла равен 5/10=0,5. Это косинус угла 60º.
4
Определите косинус угла по его значениям для других тригонометрический функций. Если известен синус угла α то его косинус посчитайте, отняв от числа 1 квадрат синуса, а из полученного результата извлеките квадратный корень cos(α)=√(1-sin²(α)). Например, если синус угла равен 0,6, то используя известную формулу, получите cos(α)=√(1-0,6²)=√(1-0,36)= √0,64=0,8.
5
Вычислите косинус при известном тангенсе угла. Для этого число 1 поделите на сумму 1 и квадрата тангенса, а из полученного результата извлеките квадратный корень: cos(α)=√(1/(1+tg²(α))). Например, если тангенс угла равен 1, то его косинус cos(α)=√(1/(1+1²))=1/√2.