Как понять тригонометрию

Мало кто в школе любил алгебру. Многим уже состоявшимся людям так и не удалось понять смысл этой "науки с непонятными крючочками". Но так или иначе, а сдавать ЕГЭ по математике придется всем, кому сейчас нет 18. Поэтому школьникам, которые так и не поняли, что же такое тригонометрия и эти"непонятные" синусы, косинусы, тангенсы стоит попытаться в это вникнуть.

Вам понадобится

• Листок бумаги, линейка, циркуль, чертежная бумага миллиметровка.

Инструкция

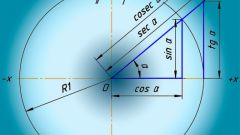
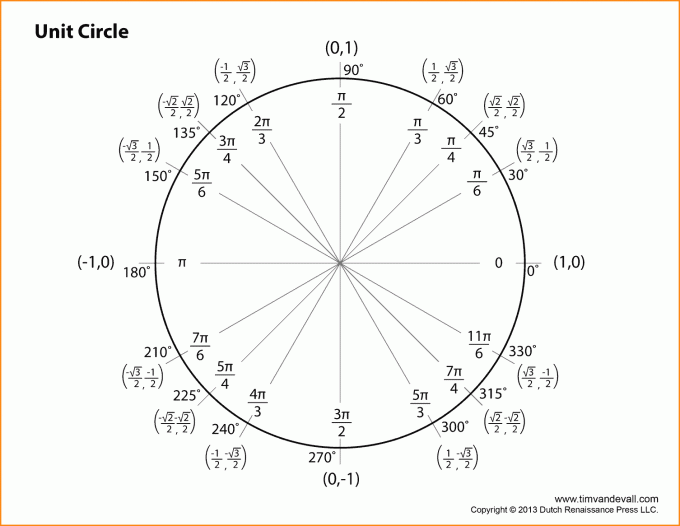
1. Для начала нужно понять, что вся тригонометрия заключена в прямоугольном треугольнике и таких базовых понятиях, как катеты, гипотенуза, единичная окружность. И, безусловно, не стоит забывать о теореме Пифагора, которая наиболее тесно связана с тригонометрией.
   
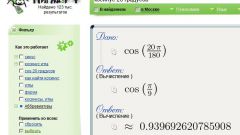
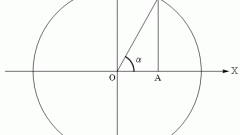
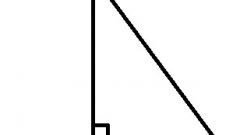
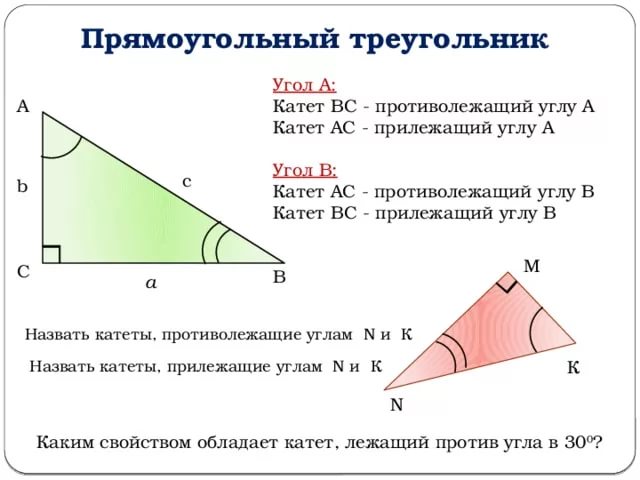
2. Перейдем к описанию тригонометрических функций. Все пояснения будут завязаны на вышеописанном рисунке. Примем за угол z угол при вершине В. Тогда синус угла z будет равен отношению противолежащего катета к гипотенузе.
   Иными словами sin(z)= b/c (см. рис.). Аналогично можно дать определение косинуса угла z: отношение прилежащего катета к гипотенузе. Или: cos(z)= a/c.
   
3. Не откладываем рисунок далеко и переходим к тангенсу. Тангенсом угла z называет отношение синуса угла z к косинусу угла z или иными словами отношение противолежащего катета к прилежащему.
   Формула tg(z)= b/a.
   Котангенс же является тангенсом, возведенным в минус первую степень, что позволяет дать ему следующее определение: котангенс угла z есть отношение прилежащего катета к противолежащему.
   Формула ctg(z)=a/b.
4. Можно сказать, что вся школьная тригонометрия основана на этих четырех понятиях. Остальные функции, такие как арксинус,арккосинус, арктангенс, арккотангенс и т. д. являются производными от вышеизложенных.