Вам понадобится
- окружность, прямоугольный треугольник
Инструкция
1
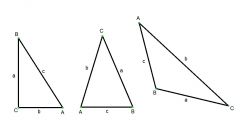
Пусть в прямоугольном треугольнике угол B - прямой. AC будет являться гипотенузой этого треугольника, стороны AB и BC - его катетами. Синусом острого угла BAC будет называться отношение противолежащего к этому углу катета BC к гипотенузе AC. То есть sin(BAC) = BC/AC.
Косинусом острого угла BAC будет называться отношение прилежащего к этому углу катета BC к гипотенузе AC. То есть cos(BAC) = AB/AC. Косинус угла можно также выразить через синус угла с помощью основного тригонометрического тождества: ((sin(ABC))^2)+((cos(ABC))^2) = 1. Тогда cos(ABC) = sqrt(1-(sin(ABC))^2).
Тангенсом острого угла BAC будет называться отношение противолежащего к этому углу катета BC к прилежащему к этому углу катету AB. То есть tg(BAC) = BC/AB. Тангенс угла также можно выразить через его синус и косинус по формуле: tg(BAC) = sin(BAC)/cos(BAC).
Косинусом острого угла BAC будет называться отношение прилежащего к этому углу катета BC к гипотенузе AC. То есть cos(BAC) = AB/AC. Косинус угла можно также выразить через синус угла с помощью основного тригонометрического тождества: ((sin(ABC))^2)+((cos(ABC))^2) = 1. Тогда cos(ABC) = sqrt(1-(sin(ABC))^2).
Тангенсом острого угла BAC будет называться отношение противолежащего к этому углу катета BC к прилежащему к этому углу катету AB. То есть tg(BAC) = BC/AB. Тангенс угла также можно выразить через его синус и косинус по формуле: tg(BAC) = sin(BAC)/cos(BAC).
2
В прямоугольных треугольниках можно рассматривать только острые углы. Для рассмотрения прямых углов необходимо вводить окружность.
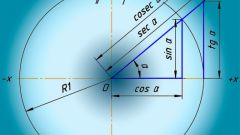
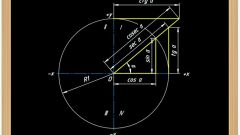
Пусть O - центр декартовой системы координат с осями X (ось абцисс) и Y (ось ординат), а также центр окружности радиуса R. Отрезок OB будет являться радиусом этой окружности. Углы можно измерить как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначьте за xB, ординату - за yB.
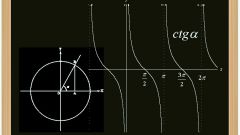
Тогда синус угла определяется как yB/R, косинус угла - xB/R, тангенс угла tg(x) = sin(x)/cos(x) = yB/xB.
Пусть O - центр декартовой системы координат с осями X (ось абцисс) и Y (ось ординат), а также центр окружности радиуса R. Отрезок OB будет являться радиусом этой окружности. Углы можно измерить как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точки В обозначьте за xB, ординату - за yB.
Тогда синус угла определяется как yB/R, косинус угла - xB/R, тангенс угла tg(x) = sin(x)/cos(x) = yB/xB.
3
Косинус угла можно рассчитать и в любом треугольнике, если известны длины всех его сторон. По теореме косинусов AB^2 = ((AC)^2)+((BC)^2)-2*AC*BC*cos(ACB). Отсюда, cos(ACB) = ((AC^2)+(BC^2)-(AB^2))/(2*AC*BC).
Синус и тангенс этого угла можно вычислить из приведенных выше определения тангенса угла и основного тригонометрического тождества.
Синус и тангенс этого угла можно вычислить из приведенных выше определения тангенса угла и основного тригонометрического тождества.
Источники:
- рассчитать косинус