Инструкция
1
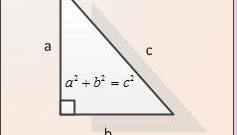
Если известна величина одного из двух острых углов (β) прямоугольного треугольника, то для нахождения другого (α) больше ничего не нужно. Используйте теорему о сумме углов треугольника в евклидовой геометрии - так как она (сумма) всегда равна 180°, то рассчитайте величину недостающего угла вычитанием величины известного острого угла из 90°: α=90°-β.
2
Если кроме величины одного из острых углов (β) известны длины обоих катетов (А и В), то можно использовать и другой способ вычисления - с помощью тригонометрических функций. Согласно теореме синусов отношения длин каждого из катетов к синусу противолежащего угла одинаковы, поэтому синус нужного угла (α) находите делением длины прилежащего к нему катета на длину второго катета с последующим умножением результата на синус известного острого угла. Тригонометрическая функция, преобразующая значение синуса в соответствующую этому значению величину в угловых градусах, называется арксинусом - примените ее к полученному выражению и вы получите окончательную формулу: α=arcsin(sin(β)*А/В).
3
Если известны лишь длины обоих катетов (А и В), то их соотношения позволят получить тангенс или котангенс (в зависимости от того, что поставить в числитель) вычисляемого угла (α). Применяйте к этим соотношениям соответствующие им обратные функции: α = arctg(А/В) = arcctg(В/А).
4
Если известны только длина (С) гипотенузы (самой длиной стороны) и катета (В), прилежащего к вычисляемому углу (α), то отношение этих длин даст значение косинуса искомого угла. Как и для остальных тригонометрических функций, существует функция обратная косинусу (арккосинус) которая поможет из этого соотношения вывести величину угла в градусах: α=arcsin(В/С).
5
При тех же исходных данных, что и в предыдущем шаге, можно воспользоваться и вовсе экзотической тригонометрической функцией - секанс. Она получается делением длины гипотенузы (С) на длину прилежащего к нужному углу катета (В) - находите арксеканс от этого соотношения дли вычисления величины прилегающего к катету угла: α=arcsес(С/В).