Как найти гипотинузу в треугольнике

Гипотенузой называется самая длинная сторона прямоугольного треугольника. Она противолежит самому большому углу, то есть прямому. Подобные вычисления применяются на практике. Необходимость вычислить гипотенузу возникает в строительстве - при расчете лестниц, в геодезиии и картографии — при определении протяженности склона. Подобная задача регулярно возникает и в повседневной жизни. Например, для того, чтобы определить длину растяжек для палатки.

Вам понадобится

• - прямоугольный треугольник с заданными параметрами;
• - калькулятор;
• - карандаш;
• - линейка;
• - угольник;
• - теорема Пифагора;
• - определения синуса и косинуса.

Инструкция

1. Постройте прямоугольный треугольник. В условиях задачи должны быть даны либо величины обоих катетов, либо длина катета и размер одного из углов. Зная эти данные и используя их соотношения, можно вычислить и все остальные параметры. Начните с построения треугольника. Это не только поможет вам в вычислениях, но и даст возможность запомнить способы решения подобных задач на очень долгое время.
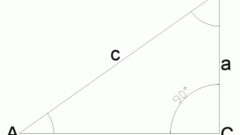
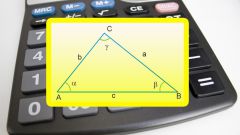
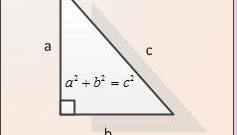
2. На листе бумаги проведите горизонтальную прямую и отложите на ней размер одного из катетов. К начальной точке отрезка проведите перпендикуляр. Следующие построения выполняйте в зависимости от того, какие данные у вас есть. Если вы знаете размеру обоих катетов, на перпендикуляре отложите отрезок, равный длине второго. Соедините полученную точку с концом первого отрезка. Обозначьте прямой угол как С, а острые — как А и В. Обозначьте противолежащие углам стороны как а, b и с.
3. Если вам известен катет и один из углов, начертите точно такой же отрезок. К начальной точке проведите перпендикуляр, а от конечной отложите заданный или вычисленный размер прилежащего угла. Обозначьте треугольник и его элементы точно так же, как и в предыдущем случае.
4. Зная оба катета, вычислите гипотенузу по теореме Пифагора. Она равна квадратному корню из суммы квадратов катетов, то есть с=√a2+b2. Это выражение является частным случаем общей формулы вычисления стороны треугольника. Она равна квадратному корню из суммы квадратов двух других стороны, минус удвоенное произведение этих сторон на косинус угла между ними. То есть с=√a2+b2-2ab*cosC. Поскольку косинус прямого угла равен нулю, то и его произведение на любое число равно нулю.
5. Зная катет и противолежащий или прилежащий угол, найдите гипотенузу через синус или косинус. В первом случае формула будет выглядеть как с=а/sinA, где с — гипотенуза, а — длина известного катета, А — противолежащий угол. Во втором случае выражение можно представить как с=а/cosB, где B – прилежащий угол.