Инструкция
1
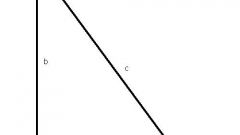
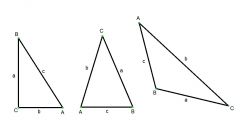
Пусть задан треугольник с вершинами A, B и C, причем угол ABC — прямой, то есть равен девяноста градусам. Стороны AB и BC такого треугольника называются катетами, а сторона АC — гипотенузой. Для начала посмотрите условия задачи и определите, величины каких из сторон треугольника вам известны, а какую сторону требуется найти. Для успешного решения задачи нужно знать длины двух из трех сторон треугольника. Вам должны быть известны либо длины двух катетов, либо длина одного из катетов и длина гипотенузы.
2
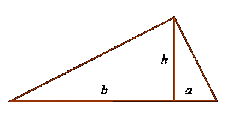
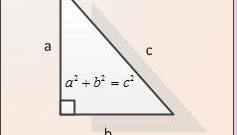
Длина сторон прямоугольного треугольника рассчитывается по теореме древнегреческого математика Пифагора. Эта теорема задает зависимость между катетами и гипотенузой: квадрат гипотенузы равен сумме квадратов катетов. В случае, если требуется найти величину катета (например, катета AB), формула для нее будет выглядеть так: AB = √(AC² - BC²). Вычислить ее можно на калькуляторе, но в некоторых случаях можно и в уме. Например, для треугольника со сторонами BC = 4 и AC = 5 величина катета AB также является целым числом и поэтому легко может быть вычислена по приведенной формуле. AB = √(25 - 16) = 3.
3
Если же требуется найти длину гипотенузы, то это можно сделать по следующей формуле, выводимой из теоремы Пифагора: AC = √(AB² + BC²). Так, для треугольника со сторонами AB = 5 и BC = 12, получаем результат AC = √(25 + 144) = 13. В зависимости от условий задачи используйте полученный результат в дальнейших вычислениях или напишите в качестве вашего ответа.
Обратите внимание
В математике часто бывает неуместным вычисление точных значений квадратных и кубических корней. Если полученный по формуле результат не является целым или дробным числом, лучше оставить символ квадратного корня, а не считать ответ на калькуляторе. Например, записать ответ как AC = √7 вместо того, чтобы вычислять его значение — 2,6457.