Инструкция
1
Один из способов вычисления длин сторон произвольного треугольника предполагает использование теоремы синусов. Согласно ей соотношения длин сторон и синусов противолежащих им углов треугольника равны. Это позволяет вывести формулу длины стороны для тех случаев, когда из условий задачи известна хотя бы одна сторона и два угла в вершинах фигуры. Если ни один из этих двух углов (α и β) не лежит между известной стороной А и вычисляемой В, то умножьте длину известной стороны на синус прилегающего к ней известного угла β и разделите на синус другого известного угла а: В = А*sin(β)/sin(α).
2
Если один (γ) из двух (α и γ) известных углов образован сторонами, длина одной из которых (А) дана в условиях, а вторую (В) требуется вычислить, то примените ту же теорему. Решение можно свести к формуле, полученной в предыдущем шаге, если вспомнить еще и теорему о сумме углов в треугольнике - эта величина всегда равна 180°. В формуле неизвестен угол β, который по этой теореме можно вычислить, если отнять от 180° величины двух известных углов. Подставьте это значение в равенство, и вы получите формулу В = А*sin(180°-α-γ)/sin(α).
3
Для исходных условий, в которых даны длины двух сторон (А и В) и величина угла между ними (γ), подходит теорема косинусов, позволяющая найти длину третьей стороны (С). Для этого длины известных сторон возведите в квадрат и сложите, а от полученного результата отнимите их удвоенное произведение, умноженное на косинус угла известной величины. Из полученного таким способом числа надо извлечь квадратный корень: С = √(А²+В²-2*А*В*cos(γ)).
4
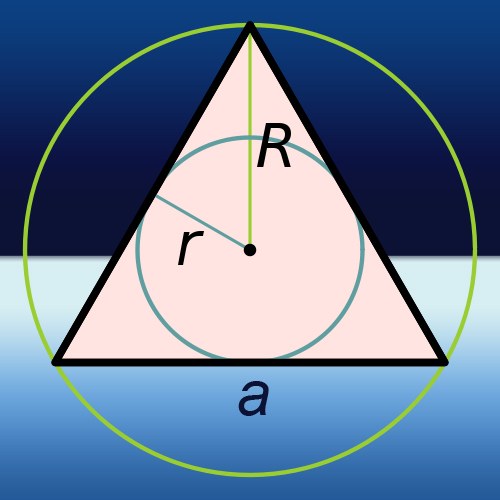
Если треугольник можно вписать в окружность известного радиуса R, а в условиях дана величина угла α, лежащего напротив стороны А, длину которой надо вычислить, то формула будет достаточно простой. Найдите произведение радиуса на синус известного угла и удвойте результат: А = 2*R*sin(α).