Инструкция
1
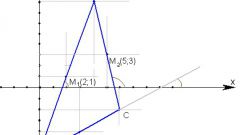
По двум сторонам и углу между ними
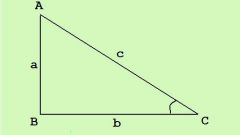
Если известны длины двух сторон треугольника и величина угла между ними, то найти длину третьей стороны можно воспользовавшись теоремой косинусов: квадрат длины стороны треугольника равняется сумме квадратов длин двух его других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Отсюда имеем:
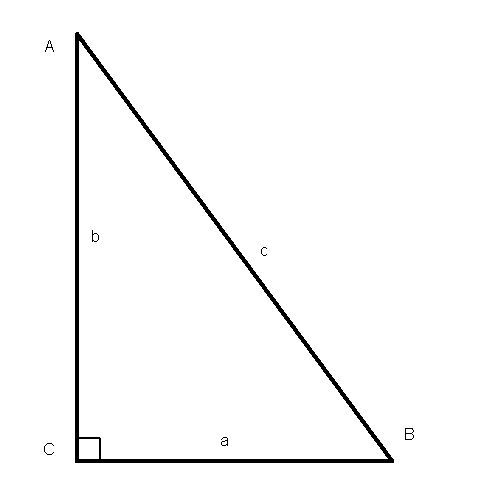
с=√(а²+b²-2аb*cosC), где
а и b – длины известных сторон,
С – величина угла, заключенного между этими сторонами (противолежащего искомой стороне),
с – длина искомой стороны.
Пример 1.
Дан треугольник со сторонами 10 см и 20 см и углом между ними равным 60 градусов. Найти длину стороны.
Решение.
По вышеприведенной формуле получаем:
с=√(10²+20²-2*10*20*cos60º)=√(500-200)=√300~17,32
Ответ: длина стороны треугольника, противолежащей сторонам длинами 10 и 20 сантиметров и величиной угла между ними 60º - ~17,32 см.
Если известны длины двух сторон треугольника и величина угла между ними, то найти длину третьей стороны можно воспользовавшись теоремой косинусов: квадрат длины стороны треугольника равняется сумме квадратов длин двух его других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Отсюда имеем:
с=√(а²+b²-2аb*cosC), где
а и b – длины известных сторон,
С – величина угла, заключенного между этими сторонами (противолежащего искомой стороне),
с – длина искомой стороны.
Пример 1.
Дан треугольник со сторонами 10 см и 20 см и углом между ними равным 60 градусов. Найти длину стороны.
Решение.
По вышеприведенной формуле получаем:
с=√(10²+20²-2*10*20*cos60º)=√(500-200)=√300~17,32
Ответ: длина стороны треугольника, противолежащей сторонам длинами 10 и 20 сантиметров и величиной угла между ними 60º - ~17,32 см.
2
По двум углам и стороне
Если известны величины двух углов и длина одной сторон треугольника, то длины двух остальных сторон удобнее всего находить воспользовавшись теоремой синусов: отношение синусов углов треугольника к длинам противолежащих сторон равны между собой.
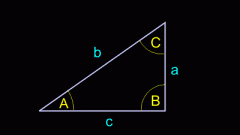
sinA/a=sinB/b=sinC/с, где:
a, b, c – длины сторон треугольника, а A, B, C – величины противолежащих углов.
Какие именно углы треугольника известны – не важно, так как, воспользовавшись тем фактом, что сумма углов треугольника равна 180 градусов, можно легко узнать величину неизвестного угла.
То есть, например, если известны величины углов А и С и длина стороны а, то длина стороны с будет:
с=а*sinC/sinA
Если известны величины двух углов и длина одной сторон треугольника, то длины двух остальных сторон удобнее всего находить воспользовавшись теоремой синусов: отношение синусов углов треугольника к длинам противолежащих сторон равны между собой.
sinA/a=sinB/b=sinC/с, где:
a, b, c – длины сторон треугольника, а A, B, C – величины противолежащих углов.
Какие именно углы треугольника известны – не важно, так как, воспользовавшись тем фактом, что сумма углов треугольника равна 180 градусов, можно легко узнать величину неизвестного угла.
То есть, например, если известны величины углов А и С и длина стороны а, то длина стороны с будет:
с=а*sinC/sinA
3
Если при таких же исходных данных необходимо найти длину стороны b, то чтобы воспользоваться теоремой синусов, нужно знать величину угла В:
так как В=180º-А-С, то длина стороны b можно будет найти по формуле:
b=a*sin(180º-А-С)/sinA
Пример 2.
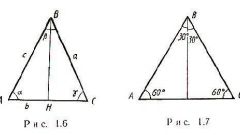
Пусть в треугольнике ABC известны длина стороны а=10 см и величины углов А=30 и С=20. Найти длину стороны b.
Решение: по полученной выше формуле получаем:
b=10*sin(180º-30º-20º)/sin30º=10*sin130º/0,5=5*sin130º~3,83
Ответ: длина стороны треугольника ~3,83 см.
так как В=180º-А-С, то длина стороны b можно будет найти по формуле:
b=a*sin(180º-А-С)/sinA
Пример 2.
Пусть в треугольнике ABC известны длина стороны а=10 см и величины углов А=30 и С=20. Найти длину стороны b.
Решение: по полученной выше формуле получаем:
b=10*sin(180º-30º-20º)/sin30º=10*sin130º/0,5=5*sin130º~3,83
Ответ: длина стороны треугольника ~3,83 см.
Видео по теме
Источники:
- треугольник противолежащие стороны
- Как по двум сторонам прямоугольного треугольника найти