Как вычислить длину стороны треугольника

Для вычисления длин сторон в произвольном треугольнике чаще всего приходится применять теоремы синусов и косинусов. Но среди всего множества произвольных многоугольников этого рода существуют их «более правильные» вариации - равносторонние, равнобедренные, прямоугольные. Если о треугольнике известно, что он принадлежит к одной из этих разновидностей, способы вычисления его параметров значительно упрощаются. При вычислении длин их сторон часто можно обойтись без тригонометрических функций.

Инструкция

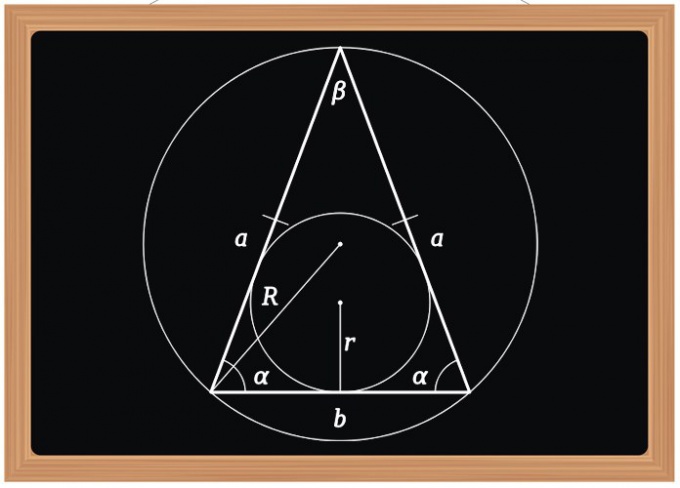
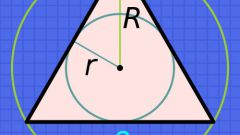
1. Длину стороны (А) равностороннего треугольника можно найти по радиусу вписанной в него окружности (r). Для этого увеличьте ее в шесть раз и разделите на квадратный корень из тройки: А = r*6/√3.
2. Зная радиус описанной окружности (R), тоже можно вычислить длину стороны (А) правильного треугольника. Этот радиус вдвое больше использованного в предыдущей формуле, поэтому утройте его и тоже поделите на квадратный корень из тройки: А = R*3/√3.
3. По периметру (Р) равностороннего треугольника вычислить длину его стороны (А) еще проще, так как длины сторон в этой фигуре одинаковы. Просто разделите периметр натрое: А = Р/3.
4. В равнобедренном треугольнике вычисление длины стороны по известному периметру немного сложнее - нужно знать еще и длину хотя бы одной из сторон. Если известна длина стороны А, лежащей в основании фигуры, длину любой из боковых (В) находите делением пополам разности между периметром (Р) и размером основания: В = (Р-А)/2. А если известна боковая сторона, то длину основания определяйте вычитанием из периметра удвоенной длины боковой: А = Р-2*В.
5. Знания площади (S), занимаемой на плоскости правильным треугольником, тоже достаточно для нахождения длины его стороны (А). Извлеките квадратный корень из соотношения площади и квадратного корня из тройки, а полученный результат удвойте: А = 2*√(S/√3).
6. В прямоугольном треугольнике, в отличие от любого другого, для вычисления длины одной из сторон достаточно знать длины двух других. Если искомая сторона - гипотенуза (С), для этого находите квадратный корень из суммы длин известных сторон (А и В), возведенных в квадрат: С = √(А²+В²). А если вычислить требуется длину одного из катетов, то квадратный корень следует извлекать из разности квадратов длин гипотенузы и другого катета: А = √(С²-В²).