Инструкция
1
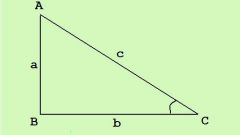
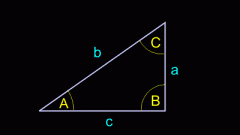
Стороны треугольника, как и других многоугольников, имеют собственные названия: боковые стороны, основание, а также гипотенуза и катеты у фигуры с прямым углом. Это облегчает расчеты и формулы, делая их более очевидными даже если треугольник произвольный. Фигура графическая, поэтому ее всегда можно расположить так, чтобы сделать решение задачи более наглядным.
2
Стороны любого треугольника связаны между собой и другими его характеристиками различными соотношениями, которые помогают вычислить требуемую величину в одно или несколько действий. При этом чем сложнее задача, тем длиннее последовательность шагов.
3
Решение упрощается, если треугольник стандартный: слова «прямоугольный», «равнобедренный», «равносторонний» сразу выделяют определенную взаимосвязь между его сторонами и углами.
4
Длины сторон в прямоугольном треугольнике связаны между собой теоремой Пифагора: сумма квадратов катетов равна квадрату гипотенузы. А углы, в свою очередь, связаны со сторонами теоремой синусов. Она утверждает равенство отношений между длинами сторон и тригонометрической функцией sin противолежащего угла. Впрочем, это верно для любого треугольника.
5
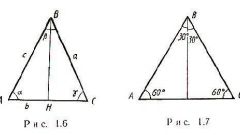
Две стороны равнобедренного треугольника равны между собой. Если их длина известна, вполне достаточно еще только одной величины, чтобы найти третью. Например, пусть известна высота, проведенная к ней. Этот отрезок делит третью сторону на две равные части и выделяет два прямоугольных треугольниках. Рассмотрев один из них, по теореме Пифагора найдите катет и умножьте на 2. Это и будет длина неизвестной стороны.
6
Сторону треугольника можно найти через другие стороны, углы, длины высоты, медианы, биссектрисы, величину периметра, площади, радиус вписанной окружности и т.д. Если нельзя сразу применить одну формулу, то произведите ряд промежуточных вычислений.
7
Рассмотрите пример: найдите сторону произвольного треугольника, зная медиану ma=5, проведенную к ней, и длины двух других медиан mb=7 и mc=8.
8
РешениеЗадача предполагает использование формул для медианы. Найти нужно сторону а. Очевидно, следует составить три уравнения с тремя неизвестными.
9
Запишите формулы для всех медиан:ma = 1/2•√(2•(b² + c²) – a²) = 5;mb = 1/2•√(2•(a² + c²) – b²) = 7;mc = 1/2•√(2•(a² + b²) – c²) = 8.
10
Выразите c² из третьего уравнения и подставьте ее во второе:c² = 256 – 2•a² – 2•b² b² = 20 → c² = 216 – a².
11
Возведите обе стороны первого уравнения в квадрат и найдите a, введя выраженные величины:25 = 1/4•(2•20 + 2•(216 – a²) – a²) → a ≈ 11,1.
Источники:
- стороны треугольника это