Инструкция
1
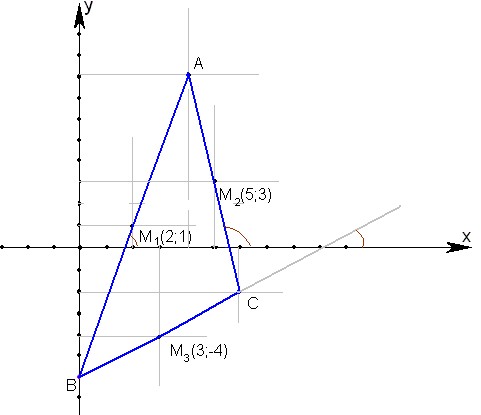
Вам заданы координаты трех точек. Обозначим их как (x1, y1), (x2, y2), (x3, y3). Предполагается, что эти точки являются вершинами некоторого треугольника. Задача состоит в том, чтобы составить уравнения его сторон — точнее уравнения тех прямых, на которых лежат эти стороны. Эти уравнения должны иметь вид:
y = k1*x + b1;
y = k2*x + b2;
y = k3*x + b3.Таким образом, вам предстоит найти угловые коэффициенты k1, k2, k3 и смещения b1, b2, b3.
2
Убедитесь, что все точки различны между собой. Если какие-то две совпадают, то треугольник вырождается в отрезок.
3
Найдите уравнение прямой, проходящей через точки (x1, y1), (x2, y2). Если x1 = x2, то искомая прямая вертикальна и ее уравнение x = x1. Если y1 = y2, то прямая горизонтальна и ее уравнение y = y1. В общем случае эти координаты не будут равны друг другу.
4
Подставляя координаты (x1, y1), (x2, y2) в общее уравнение прямой, вы получите систему из двух линейных уравнений:k1*x1 + b1 = y1;
k1*x2 + b1 = y2.Вычтите одно уравнение из другого и решите полученное уравнение относительно k1:k1*(x2 - x1) = y2 - y1, следовательно, k1 = (y2 - y1)/(x2 - x1).
5
Подставляя найденное выражение в любое из исходных уравнений, найдите выражение для b1:((y2 - y1)/(x2 - x1))*x1 + b1 = y1;
b1 = y1 - ((y2 - y1)/(x2 - x1))*x1.Поскольку уже известно, что x2 ≠ x1, можно упростить выражение, умножив y1 на (x2 - x1)/(x2 - x1). Тогда для b1 вы получите следующее выражение:b1 = (x1*y2 - x2*y1)/(x2 - x1).
6
Проверьте, не лежит ли третья из заданных точек на найденной прямой. Для этого подставьте значения (x3, y3) в выведенное уравнение и посмотрите, соблюдается ли равенство. Если оно соблюдается, следовательно, все три точки лежат на одной прямой, и треугольник вырождается в отрезок.
7
Тем же способом, что описан выше, выведите уравнения для прямых, проходящих через точки (x2, y2), (x3, y3) и (x1, y1), (x3, y3).
8
Окончательный вид уравнений для сторон треугольника, заданного координатами вершин, выглядит так:(1) y = ((y2 - y1)*x + (x1*y2 - x2*y1))/(x2 - x1);
(2) y = ((y3 - y2)*x + (x2*y3 - x3*y2))/(x3 - x2);
(3) y = ((y3 - y1)*x + (x1*y3 - x3*y1))/(x3 - x1).