Инструкция
1
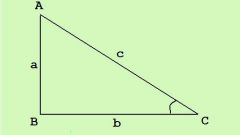
Если известны величины двух углов треугольника (α и β), а также длина одной из сторон (C), то длины двух других сторон можно определить, но формулы вычисления будут отличаться, в зависимости от того, прилегают ли оба известных угла к стороне известной длины. Если да, то, исходя из теоремы синусов и учитывая теорему о сумме углов в треугольнике, длину той стороны (A), которая лежит напротив угла α, можно определить как отношение произведения синуса этого угла на известную длину стороны к синусу разницы между развернутым углом (180°) и суммой двух известных углов: A=sin(α)∗C/(sin(180°-α-β)). Для определения длины третьей стороны (B), лежащей напротив угла β эту формулу надо изменить соответствующим образом: B=sin(β)∗C/(sin(180°-α-β)).
2
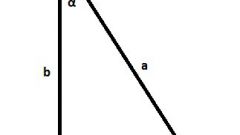
Если сторона (B) известной длины не лежит между двумя известными углами (α и β), а примыкает только к одному из них (например, к α), то формулы вычисления длин оставшихся сторон изменятся. Сторона (C), лежащая напротив неизвестного, угла будет иметь длину, определяемую соотношением произведения синуса угла, недостающего до суммарной величины всех углов в 180°, на длину известной стороны к синусу угла, лежащего напротив нее: C=sin(180°-α-β)∗B/sin(β). А длина третьей стороны (A) может быть определена по этой формуле: A=sin(α)∗B/sin(β).
3
Если известны длины двух сторон (A и B) и величина одного из углов, то для нахождения длины недостающей стороны можно воспользоваться теоремой косинусов. Если угол известной величины (γ) лежит между известными сторонами, то длина искомой стороны (C) будет равна квадратному корню из разницы между суммой квадратов длин известных сторон и удвоенным произведением длин этих сторон на косинус известного угла: C=√(А²+B²-2∗А∗B∗cos(γ)).