Как найти стороны прямоугольного треугольника

Соотношения между сторонами и углами прямоугольного треугольника рассматриваются в разделе математики, который называется тригонометрией. Для нахождения сторон прямоугольного треугольника достаточно знать теорему Пифагора, определения тригонометрических функций, и иметь какое-либо средство для нахождения значений тригонометрических функций, например, калькулятор или таблицы Брадиса. Рассмотрим ниже основные случаи задач нахождения сторон прямоугольного треугольника.

Вам понадобится

• Калькулятор, таблицы Брадиса.

Инструкция

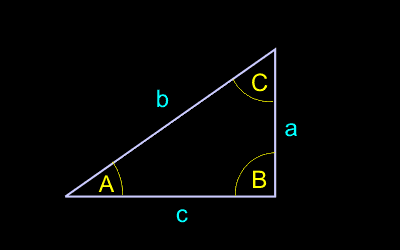
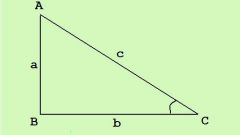
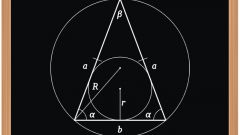
1. Примем следующие обозначения:
   
   с – длина гипотенузы (стороны, противолежащей прямому углу);
   
   a, b – длины катетов (сторон, прилежащих к прямому углу);
   
   A – угол, противолежащий катету a;
   
   В – угол, противолежащий катету b.
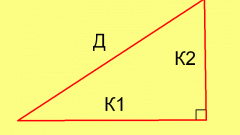
2. В случае, когда вам известны гипотенуза с и один из катетов (например, катет а), второй катет можно вычислить из теоремы Пифагора: b=sqrt(с^2-а^2). Здесь и далее «sqrt» – операция извлечения квадратного корня, «^2» - операция возведения в квадрат.
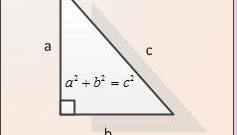
3. Если известны оба катета, гипотенуза находится также из теоремы Пифагора: с=sqrt(а^2+b^2).
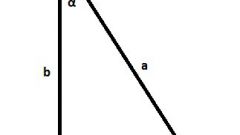
4. Если вам задан один из острых углов, например, A, и гипотенуза, то катеты можно найти из определений основных тригонометрических функций:
   
   a= c*sin(A), b= c*cos(A).
5. Если задан один из острых углов, например, A, и один из катетов, например, a, то гипотенуза и другой катет вычисляются из соотношений: b=a*tg(A), c=a*sin(A).