Как найти катет в прямоугольном треугольнике

Прежде чем мы рассмотрим различные способы нахождения катета в прямоугольном треугольнике, примем некоторые обозначения. Катетом называют прилежащую к прямому углу сторону прямоугольного треугольника. Длины катетов условно обозначим a и b. Углы, противолежащие катетам a и b обозначим соответственно через A и B. Гипотенуза, по определению, это сторона прямоугольного треугольника, которая противоположна прямому углу (при этом с другими сторонами треугольника гипотенуза образует острые углы). Длину гипотенузы обозначим через с.

Инструкция

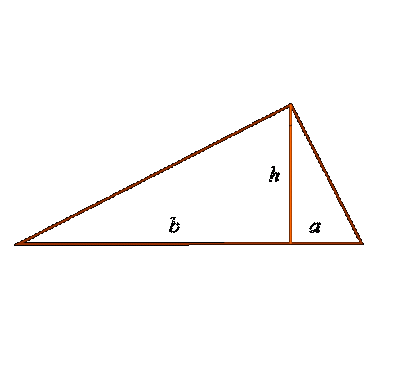
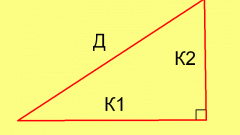
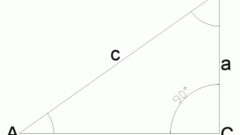
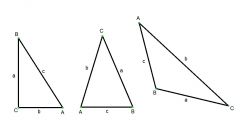
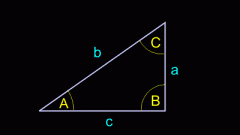
Углы, противолежащие катетам a и b обозначим соответственно через A и B. Гипотенуза, по определению, это сторона прямоугольного треугольника, которая противоположна прямому углу (при этом с другими сторонами треугольника гипотенуза образует острые углы). Длину гипотенузы обозначим через с.

Вам понадобится:
Калькулятор.

Проверьте, какому из перечисленных случаев соответствует условие вашей задачи и в зависимости от этого руководствуйтесь соответствующим пунктом. Выясните, какие величины в рассматриваемом треугольнике вам известны.

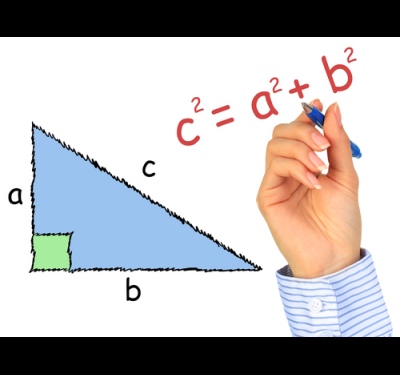
Воспользуйтесь для вычисления катета следующим выражением: a=sqrt(c^2-b^2), в том случае, если вам известны величины гипотенузы и другого катета. Это выражение получается из теоремы Пифагора, которая гласит, что квадрат гипотенузы треугольника равен сумме квадратов катетов. Оператор sqrt обозначает извлечение квадратного корня. Знак "^2" означает возведение во вторую степень.

Используйте формулу a=c*sinA, если вам известна гипотенуза (c) и угол, противолежащий искомому катету (этот угол мы обозначили, как A).
Выражение a=c*cosB используйте для нахождения катета, если вам известна гипотенуза (c) и угол, прилежащий искомому катету (этот угол мы обозначили как B).
Вычислите катет по формуле a=b*tgA в случае, когда задан катет b и угол, противолежащий искомому катету (этот угол мы условились обозначать A).

Обратите внимание:
Если же в вашей задаче катет не находится ни одним из описанных способов, скорее всего, её можно свести к какому-то из них.

Полезные советы:
Все эти выражения получаются из общеизвестных определений тригонометрических функций, поэтому, даже если вы забыли какое-то из них, вы всегда сможете путём несложных операций его быстро вывести. Также, полезно знать значения тригонометрических функций для наиболее типичных углов 30, 45, 60, 90, 180 градусов.