Обыкновенный треугольник представляет собой геометрическую фигуру, которая относится к разряду многоугольников. При этом она обладает рядом характерных особенностей, которые отличают ее от других видов многоугольников, например, параллелепипедов, пирамид и других.
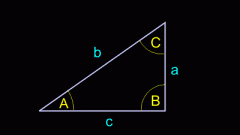
Во-первых, как следует из ее названия, она имеет три угла, которые могут иметь любую величину больше 0 и меньше 180 градусов. Во-вторых, эта фигура имеет три вершины, каждая из которых одновременно является вершиной одного из указанных трех углов. В-третьих, эта фигура имеет три стороны, которые соединяют упомянутые вершины. Таким образом, вершины, стороны и углы являются ключевыми элементами каждого треугольника, которые определяют его геометрические свойства. Кроме того, поскольку эти элементы так важны для понимания его свойств, им принято придавать обозначения, позволяющие однозначно идентифицировать каждый из элементов. Так, вершины треугольника обычно обозначают заглавными латинскими буквами, например, A, B и C. Аналогичные обозначения имеют углы треугольника, лежащие у этих вершин. Эти обозначения, в свою очередь, определяют обозначения других элементов: так, сторона треугольника, лежащая между двумя вершинами, обозначается сочетанием обозначений этих вершин. Например, сторона, лежащая между вершинами А и В, обозначается АВ.
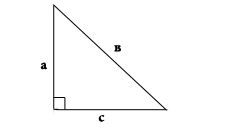
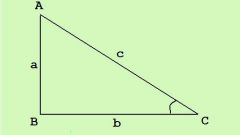
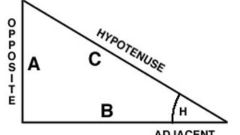
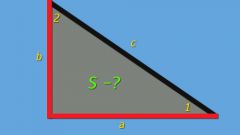
Прямоугольный треугольник - это такой тип треугольника, у которого одна из вершин составляет прямой угол, то есть равна 90 градусам. Таким образом, поскольку в традиционной геометрии сумма углов треугольника составляет 180 градусов, остальные два угла такого треугольника должны быть острыми, то есть составляющими мене 90 градусов. При этом стороны прямоугольного треугольника, в отличие от других типов этой геометрической фигуры, имеют специальные обозначения. Так, самая длинная сторона, лежащая напротив прямого угла, носит название гипотенузы. Остальные две стороны всегда бывают короче гипотенузы и называются катетами. Соотношение этих сторон определяется известной теоремой, которая по имени ее создателя носит название теоремы Пифагора. Она устанавливает, что квадрат длины гипотенузы равен сумме квадратов длин катетов прямоугольного треугольника. Так, например, если мы имеем прямоугольный треугольник со сторонами АВ, ВС и АС, в котором угол С является прямым, квадрат гипотенузы АВ будет равен сумме квадратов катетов ВС и ВС, между которыми расположен прямой угол.
Геометрические особенности треугольника
Прямоугольный треугольник
Прямоугольный треугольник - это такой тип треугольника, у которого одна из вершин составляет прямой угол, то есть равна 90 градусам. Таким образом, поскольку в традиционной геометрии сумма углов треугольника составляет 180 градусов, остальные два угла такого треугольника должны быть острыми, то есть составляющими мене 90 градусов. При этом стороны прямоугольного треугольника, в отличие от других типов этой геометрической фигуры, имеют специальные обозначения. Так, самая длинная сторона, лежащая напротив прямого угла, носит название гипотенузы. Остальные две стороны всегда бывают короче гипотенузы и называются катетами. Соотношение этих сторон определяется известной теоремой, которая по имени ее создателя носит название теоремы Пифагора. Она устанавливает, что квадрат длины гипотенузы равен сумме квадратов длин катетов прямоугольного треугольника. Так, например, если мы имеем прямоугольный треугольник со сторонами АВ, ВС и АС, в котором угол С является прямым, квадрат гипотенузы АВ будет равен сумме квадратов катетов ВС и ВС, между которыми расположен прямой угол.
Источники:
- Треугольники