Для начала договоримся об обозначениях. Катетом называют сторону прямоугольного треугольника, которая прилежит к прямому углу (т.е. составляет с другой стороной угол 90 градусов). Длины катетов условимся обозначать a и b. Величины острых углов прямоугольного треугольника, противолежащих катетам, назовём A и B соответственно. Гипотенузой называют сторону прямоугольного треугольника, которая противолежит прямому углу (т.е. находится напротив прямого угла, с другими сторонами треугольника образует острые углы). Длину гипотенузы обозначим через с. Искомую площадь обозначим через S.
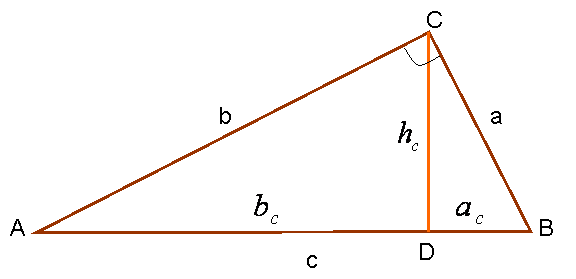
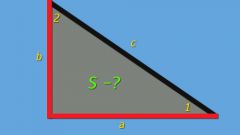
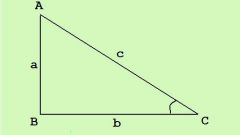
Определите, какие величины рассматриваемого прямоугольноготреугольника вам известны. Исходя из этого, выберите подходящее выражение.
2
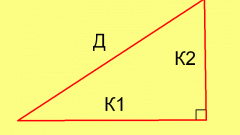
Вычислите площадь прямоугольного треугольника, как половину произведения катетов, т.е. S=0.5*a*b в том случае, если вам известны их длины.
3
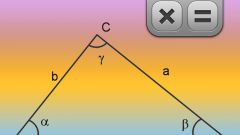
Расчитайте площадь по формуле S = b*c*sin(A)/2, если вам задан один из катетов (b), гипотенуза (с), а так же угол между ними (A). Эта формула справедлива не только для прямоугольного треугольника, но для любого треугольника вообще.
4
Примените формулу S = (a^2)/(2*tg(A)) в том случае, если вам задан только один из катетов (a), но также известен и противолежащий этому катету угол (A). Знаком "^2" обозначена операция возведения в квадрат.
5
Используйте формулу S=(a^2)*tg(B)/2 d случае, если вам задан только один из катетов (a), но также известен и прилежащий этому катету угол (B).
6
Вычислите площать по формуле S = a*sqrt(c^2 – a^2)/2, если вам известны величины катета (a) и гипотенузы (c). Операцию sqrt обозначает квадратный корень.
7
Воспользуйтесь выражением S = (c^2)*sin(A)*cos(A)/2, eсли задана гипотенуза (c) и один из острых углов (A).
Видео по теме
Источники:
"Пособие по математике для поступающих в вузы", под ред. Г.Н. Яковлева, 1982.
