Инструкция
1
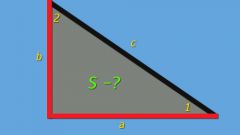
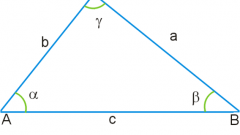
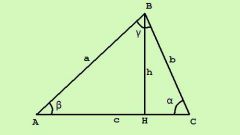
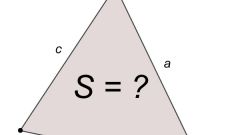
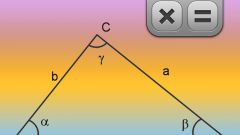
Первый вариант формулы вычисления площади треугольника (S) по известной длине одной из сторон (A) и величинам прилегающих к ней углов (α и β) предполагает вычисление котангенсов этих углов. Площадь в этом случае будет равна квадрату длины известной стороны, разделенному на удвоенную сумму котангенсов известных углов: S = A*A/(2*(ctg(α)+ctg(β))). Например, если длина известной стороны равна 15 см, а величины прилегающих к ней углов равны 40° и 60°, то расчет площади будет выглядеть так: 15*15/(2*(ctg(40)+ctg(60))) = 225/(2*(-0.895082918+3.12460562)) = 225/4.4590454 = 50.4592305 квадратных сантиметров.
2
Второй вариант вычисления площади вместо котангенсов использует синусы известных углов. В этом варианте площадь равна квадрату длины известной стороны, умноженному на синусы каждого из углов и разделенному на удвоенный синус суммы этих углов: S = A*A*sin(α)*sin(β)/(2*sin(α + β)). Например, для того же треугольника с известной стороной в 15 см, и прилегающими к ней углами в 40° и 60°, расчет площади будет выглядеть так: (15*15*sin(40)*sin(60))/(2*sin(40+60)) = 225*0.74511316*(-0.304810621)/(2*(-0.506365641)) = -51.1016411/-1.01273128 = 50.4592305 квадратных сантиметров.
3
В третьем варианте вычисления площади треугольника задействованы тангенсы углов. Площадь будет равна квадрату длины известной стороны, умноженному на тангенсы каждого из углов и деленному на удвоенную сумму тангенсов этих углов: S = A*A*tg(α)*tg(β)/2(tg(α)+tg(β)). Например, для использованного в предыдущих шагах треугольника со стороной в 15 см и прилегающими углами в 40° и 60°, расчет площади будет выглядеть так: (15*15*tg(40)*tg(60))/(2*(tg(40)+tg(60)) = (225*(-1.11721493)*0.320040389)/(2*(-1.11721493+0.320040389)) = -80.4496277/-1.59434908 = 50.4592305 квадратных сантиметров.
4
Практические расчеты можно производить, например, с помощью калькулятора поисковой системы Google. Для этого достаточно подставить в формулы числовые значения и ввести их в поле поискового запроса.