Инструкция
1
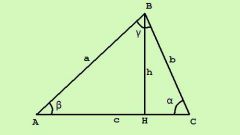
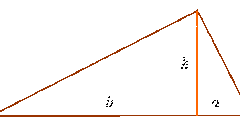
Если известна длина одной из сторон треугольника (A) и высота (Н), проведенная из этой стороны к противолежащей ей вершине, то площадь (S) произвольного треугольника можно определить, как половину произведения этих известных величин: S=A∗H/2;
2
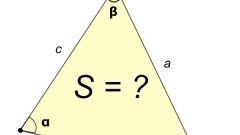
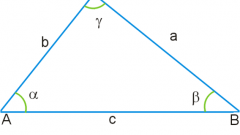
Если известны длины двух сторон треугольника (A и B) и величина угла между ними (γ), то площадь (S) треугольника будет равна половине произведения длин сторон на синус известного угла: S=A∗B∗sin(γ)/2.
3
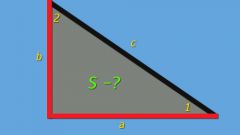
Если известны длины всех трех сторон (A, B и C) в произвольном треугольнике, то для расчета его площади (S) удобнее ввести дополнительную переменную - полупериметр (p). Эта переменная вычисляется делением пополам суммы длин всех сторон: p=(A+B+C)/2. С использованием этой переменной площадь треугольника можно определить как квадратный корень произведения полупериметра на разность этой переменной и длины каждой из сторон: S=√(p∗(p-A)∗(p-B)∗(p-C)).
4
Если кроме длин всех сторон (A, B и C) известна и длина радиуса (R) описанной возле произвольного треугольника окружности, то можно обойтись без полупериметра - площадь (S) будет равна отношению произведения длин всех сторон к учетверенному радиусу окружности: S=A∗B∗C/(4∗R).
5
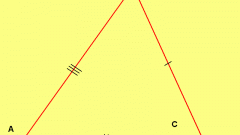
Если известны величины всех углов треугольника (α, β и γ) и длина одной из его сторон (A), то площадь (S) будет равна величине отношения произведения квадрата длины известной стороны на синусы двух углов, прилегающих к ней, к удвоенному синусу противолежащего угла: S=A²∗sin(β)∗sin(γ)/(2∗sin(α)).
6
Если известны величины всех углов произвольного треугольника (α, β и γ) и радиус (R) описанной около него окружности, то площадь (S) будет равняться удвоенному произведению квадрата радиуса на синусы всех углов: S=2∗R²∗sin(α)∗sin(β)∗sin(γ).
Видео по теме