Как посчитать площадь треугольника

По определению из геометрии, треугольником называется фигура, состоящая из трёх вершин и трёх попарно соединяющих их отрезков. Существует большое количество формул для расчёта площади треугольников, для каждого вида треугольников можно использовать специальную формулу.

Инструкция

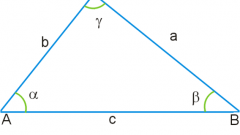
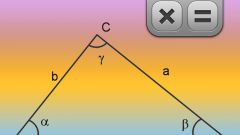
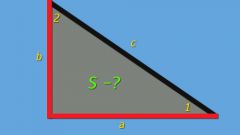
1. Площадь любого треугольника можно посчитать, зная длины его сторон по формуле Герона:
   
   S = √(p * (p - a) * (p - b) * (p - c)), где a ,b , c – стороны треугольника, p = (a + b + c)/2 – полупериметр.
   
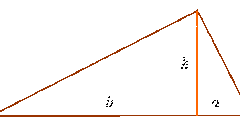
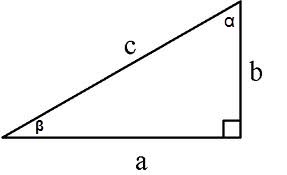
2. Площадь прямоугольного треугольника можно рассчитать несколькими способами:
   
   1. По двум катетам S = a * b/2, a, b – катеты,
   
   2. По катету и противолежащему ему углу S = a²/2tg∠α,
   
   3. По катету и прилежащему ему углу S = (a² * tg∠β)/2,
   
   4. По катету и гипотенузе S = a * √(c² - a²)/2, где c – гипотенуза, a – катет,
   
   5. По гипотенузе и прилежащим к ней углам
   
   S = (c² * sin∠α * cos∠α)/2 или S = (c² * sin∠α * sin∠β)/2
   
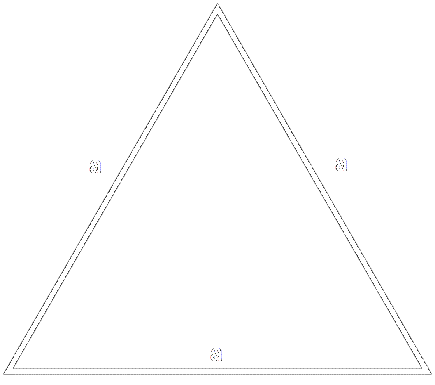
3. Для формуле
   
   S = (a² * √3)/4, где a – сторона треугольника
   
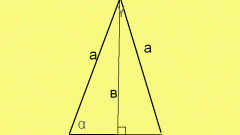
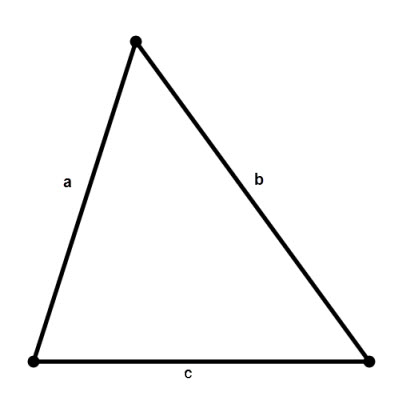
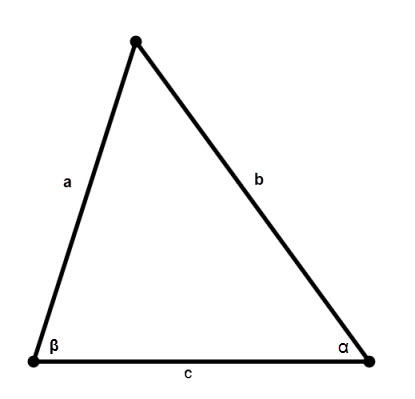
4. Если в произвольном треугольнике известна одна сторона и два прилежащих к ней угла, то её площадь вычисляется по формулам
   
   S = c²/(2 * (ctg∠α * ctg∠β)) или S = (c² * sin∠α * sin∠β)/2 * sin(∠α + ∠β)