Инструкция
1
Если длины каждой из сторон приведены в условиях задачи или у вас есть возможность самостоятельно измерить их, вычислить длину периметра будет очень просто - сложите размеры трех сторон.
2
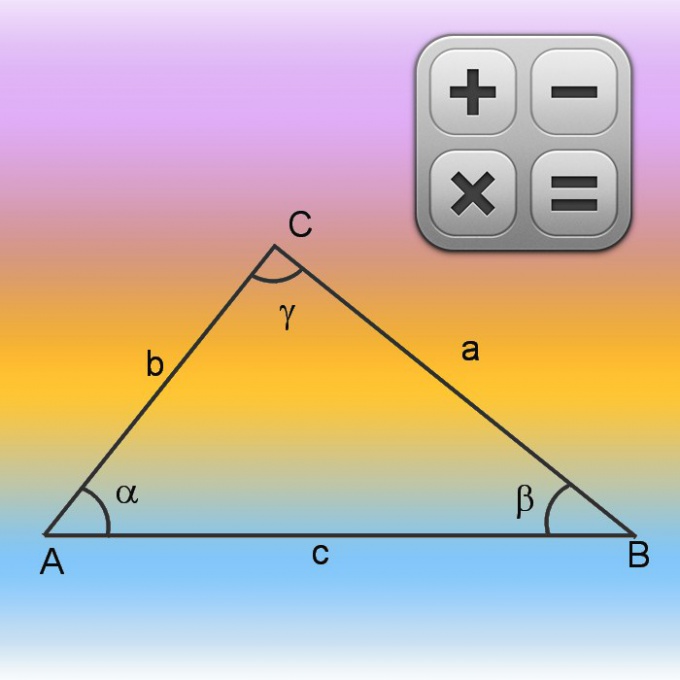
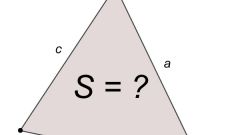
При наличии в исходных условиях информации лишь о двух сторонах (А и В), а также о величине угла между ними (γ), начните вычисление периметра (Р) с нахождения длины недостающей стороны. Сделайте это с применением теоремы косинусов. Сначала возведите в квадрат длины известных сторон и сложите результаты. Затем отнимите от полученной величины произведение длин этих же сторон друг на друга и косинус известного угла. В общем виде формулу расчета неизвестной стороны можно записать так: √(A²+B²-A*B*cos(γ)). К полученной этим способом длине третьей стороны прибавьте известные из условий длины двух других и рассчитайте периметр: Р = √(A²+B²-A*B*cos(γ)) + А + В.
3
Узнав в процессе вычисления периметра или из условий задачи длины всех сторон фигуры (А, В и С), можно приступать к вычислению ее площади (S). Эти параметры - площадь и длины сторон - связывает между собой формула Герона. Поскольку на предыдущем шаге вы уже получили формулу расчета периметра, найдите его численное значение и используйте полученную величину для упрощения формулы. Поделите периметр пополам и присвойте это значение дополнительной переменной, обозначив ее буквой p. Затем найдите разности между полупериметром и длиной каждой из сторон - всего должно получиться три значения. Эти величины перемножьте между собой и умножьте на полупериметр, а затем извлеките из рассчитанного значения квадратный корень: S=√(p∗(p-A)∗(p-B)∗(p-C)).
4
Можно использовать более простую формулу вычисления площади (S), если к полученным на предыдущих шагах длинам сторон (А, В, С) добавить радиус (R) описанной около треугольника окружности. Составьте эту формулу из произведения длин всех трех сторон, добавив к нему операцию деления на учетверенный радиус. Получиться у вас должно такое тождество: S=A∗B∗C/(4∗R).