Как найти площадь треугольника зная все его стороны

Умение вычислять площадь геометрических фигур нужно не только в стенах школы для решения задач. Оно может пригодиться и в повседневной жизни при строительстве или проведении ремонта.

Вам понадобится

• Линейка, карандаш, циркуль, калькулятор.

Инструкция

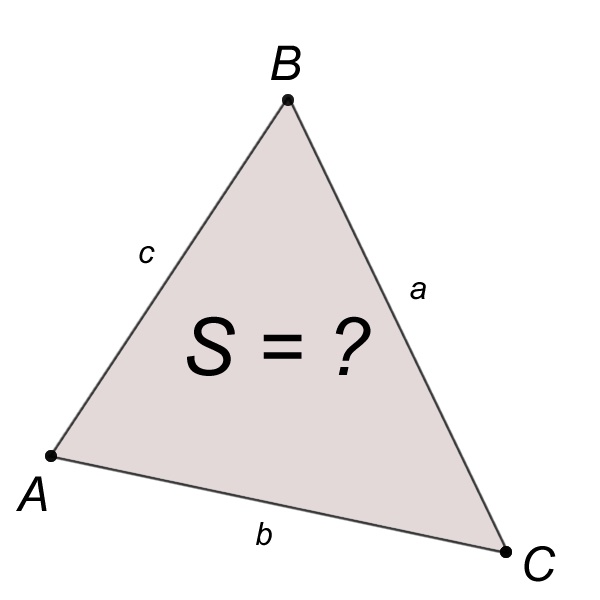
1. Стороны и углы считаются основными элементами треугольника. Треугольник полностью определяется любой из следующих троек своих основных элементов: либо тремя сторонами, либо одной стороной и двумя углами, либо двумя сторонами и углом между ними. Для существования треугольника, задаваемого тремя сторонами a, b, c, необходимо и достаточно выполнение неравенств, называемых неравенствами треугольника:
   a+b > c,
   a+c > b,
   b+c > a.
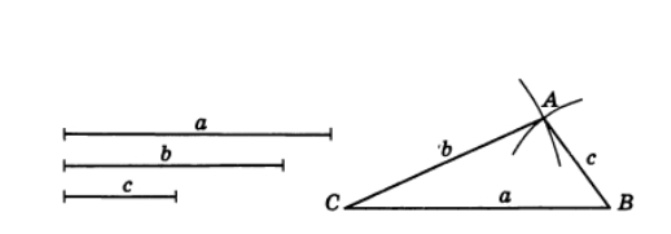
2. Для построения треугольника по трем сторонам a, b, c, необходимо из точки С отрезка СВ=a как из центра провести циркулем окружность радиусом b. Затем аналогичным образом провести из точки B окружность радиусом равным стороне c. Точка их пересечения A – третья вершина искомого треугольника ABC, где АВ=c, CB=a, CA=b - стороны треугольника. Задача имеет решение, если стороны a, b, c, удовлетворяют неравенствам треугольника указанным в шаге 1.
   
3. Площадь S, построенного таким образом треугольника ABC с известными сторонами a, b, c, вычисляется по формуле Герона:
   S=v(p(p-a)(p-b)(p-c)),
   где a, b, c – стороны треугольника, p – полупериметр.
   p = (a+b+c)/2
4. Если треугольник является равносторонним, то есть все его стороны равны (a=b=c).Площадь треугольника вычисляется по формуле:
   S=(a^2 v3)/4
5. Если треугольник является равнобедренным, то есть его боковые стороны а и b равны, а сторона с-основание. Площадь вычисляется так:
   S=c/4 v(?4a?^2-c^2 )
6. Если треугольник является равнобедренный прямоугольный, то есть боковые стороны а и b равны, угол вершины треугольника ?=90°, а углы при основании ?=?=45°. Используя числовые значения сторон, можно вычислить площадь по формуле:
   S=c^2/4=a^2/2
7. Если треугольник является прямоугольным, то есть один из его углов равен 90°, а стороны, его образующие, называются катетами, третья сторона называется гипотенузой. В данном случае площадь равняется произведению катетов, деленному на два.
   S=ab/2