Инструкция
1
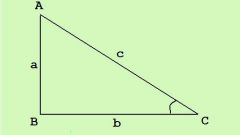
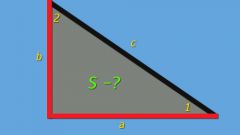
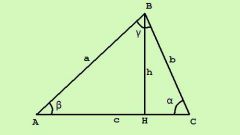
Применяйте для нахождения площади треугольника одну из формул, использующих тригонометрические функции, если известны величины одного или нескольких углов в треугольнике. Например, при известной величине угла (α) и длинам сторон, его составляющих (В и С), площадь (S) можно определить по формуле S=В*С*sin(α)/2. А при известных величинах всех углов (α, β и γ) и длине одной стороны в придачу (А) можно использовать формулу S=А²*sin(β)*sin(γ)/(2*sin(α)). Если кроме всех углов известен радиус (R) описанной окружности, то воспользуйтесь формулой S=2*R²*sin(α)*sin(β)*sin(γ).
2
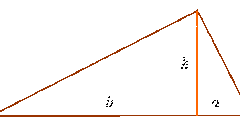
Если величины углов не известны, то для нахождения площади треугольника можно использовать формулы без тригонометрических функций. Например, если известна высота (Н), проведенная из стороны, длина которой тоже известна (А), то воспользуйтесь формулой S=А*H/2. А если даны длины каждой из сторон (А, В и С), то сначала найдите полупериметр p=(А+В+С)/2, а затем вычислите площадь треугольника по формуле S=√(p*(p-А)*(p-В)*(p-С)). Если кроме длин сторон (А, В и С) известен радиус (R) описанной окружности, то применяйте формулу S=А*В*С/(4*R).
3
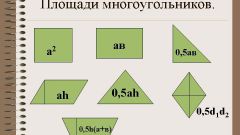
Для нахождения площади прямоугольника тоже можно задействовать тригонометрические функции - например, если известна длина его диагонали (С) и величина угла, который она составляет с одной из сторон (α). В этом случае воспользуйтесь формулой S=С²*sin(α)*cos(α). А если известны длины диагоналей (С) и величина угла, который они составляют (α), то применяйте формулу S=С²*sin(α)/2.
4
Без тригонометрических функций при нахождении площади прямоугольника можно обойтись, если известны длины его перпендикулярных сторон (А и В) - можно применить формулу S=А*В. А если дана длина периметра (P) и одной стороны (А), то воспользуйтесь формулой S=А*(P-2*А)/2.
Видео по теме