Как найти площадь треугольника

Нахождение объема треугольника действительно нетривиальная задача. Дело в том, что треугольник - двухмерная фигура, т.е. он целиком лежит в одной плоскости, а это значит, что у него попросту нет объема. Разумеется нельзя найти то, чего не существует. Но не будем опускать руки! Можно принять следующее допущение - объем двухмерной фигуры, это ее площадь. Площадь треугольника мы и будем искать.

Вам понадобится

• лист бумаги, карандаш, линейка, калькулятор

Инструкция

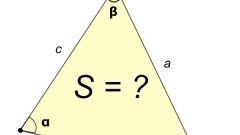
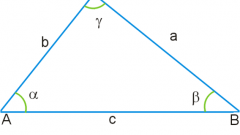
1. Начертите на листе бумаги произвольный треугольник при помощи линейки и карандаша. Внимательно рассмотрев треугольник, вы сможете убедиться, что у него действительно нет объема, так как он нарисован на плоскости. Подпишите стороны треугольника: пусть одна сторона будет стороной "а", другая - стороной "b", и третья - стороной "c". Подпишите вершины треугольника буквами "А", "B" и "C".
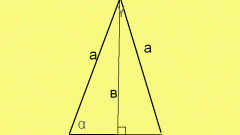
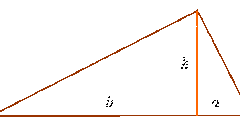
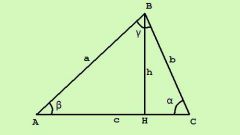
2. Измерьте линейкой любую сторону треугольника и запишите получившийся результат. После этого восстановите перпендикуляр к измеренной стороне из противоположной ей вершины, такой перпендикуляр будет являться высотой треугольника. В случае, представленном на рисунке, перпендикуляр "h" восстановлен к стороне "c" из вершины "A". Измерьте получившуюся высоту линейкой и запишите результат измерения.
3. Подсчитайте площадь треугольника, используя следующую формулу: длину стороны "c" умножьте на высоту "h" и разделите получившееся значение на 2.
4. Может случиться, что вам будет сложно восстановить точный перпендикуляр. В этом случае вам следует воспользоваться другой формулой. Измерьте все стороны треугольника линейкой. После этого подсчитайте полупериметр треугольника "p", сложив получившиеся длины сторон и разделив их сумму пополам. Имея в своем распоряжении значение полупериметра, вы можете рассчитать площадь треугольника по формуле Герона. Для этого необходимо извлечь квадратный корень из следующего выражения: p(p-a)(p-b)(p-c).
5. Вы получили искомую величину площади треугольника. Задача нахождения объема треугольника не решена, но как говорилось выше, объема у треугольника не существует. Вы можете найти объем пирамиды, которая по сути является треугольником в трехмерном мире. Если представить, что наш первоначальный треугольник стал трехмерной пирамидой, то объем такой пирамиды будет равен произведению длины ее основания на полученную нами площадь треугольника.