Инструкция
1
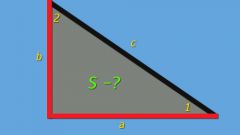
Если длины катетов (a и b) прямоугольного треугольника даны в условиях задачи в явном виде, формула расчета площади (S) фигуры будет очень проста - перемножьте эти две величины, а полученный результат разделите пополам: S = ½*a*b. Например, если длины двух коротких сторон такого треугольника составляют 30 см и 50 см, его площадь должна быть равна ½*30*50 = 750 см².
2
Если же треугольник помещен в двухмерную ортогональную координатную систему и задан координатами своих вершин A(X₁,Y₁), B(X₂,Y₂) и C(X₃,Y₃), начните с вычисления длин самих катетов. Для этого рассмотрите треугольники, составленные из каждой стороны и двух ее проекции на координатные оси. То, что эти оси перпендикулярны, позволяет найти длину стороны по теореме Пифагора, так как она является гипотенузой в таком вспомогательном треугольнике. Длины же проекций стороны (катетов вспомогательного треугольника) найдите вычитанием соответствующих координат точек, образующих сторону. Длины стороны должны быть равны |AB| = √((X₁-X₂)²+(Y₁-Y₂)²), |BС| = √((X₂-X₃)²+(Y₂-Y₃)²), |CA| = √((X₃-X₁)²+(Y₃-Y₁)²).
3
Определите, которая пара сторон является катетами - это можно сделать по их длинам, полученным на предыдущем шаге. Катеты обязаны быть короче гипотенузы. Затем воспользуйтесь формулой из первого шага - найдите половину произведения рассчитанных величин. При условии, что катетами являются стороны AB и BC, в общем виде формулу можно записать так: S = ½ * (√((X₁-X₂)²+(Y₁-Y₂)²) * √((X₂-X₃)²+(Y₂-Y₃)²).
4
Если прямоугольный треугольник помещен в трехмерную систему координат, последовательность операций не изменится. Просто добавьте в формулы расчета длин сторон третьи координаты соответствующих точек: |AB| = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²), |BС| = √((X₂-X₃)²+(Y₂-Y₃)²+(Z₂-Z₃)²), |CA| = √((X₃-X₁)²+(Y₃-Y₁)²+(Z₃-Z₁)²). Окончательная формула в этом случае должна выглядеть так: S = ½ * (√((X₁-X₂)²+(Y₁-Y₂)²+(Z₁-Z₂)²) * √((X₂-X₃)²+(Y₂-Y₃)²+(Z₂-Z₃)²).
Видео по теме