Как вычислить длину катета прямоугольного треугольника

Треугольник называется прямоугольным, если угол одной из его вершин равен 90°. Сторона, которая лежит напротив этой вершины, называется гипотенузой, а две другие - катетами. Длины сторон и величины углов в такой фигуре связаны между собой теми же соотношениями, что и в любом другом треугольнике, но так как синус и косинус прямого угла равны единице и нулю, формулы значительно упрощаются.

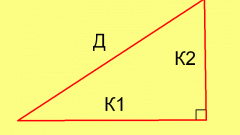
Инструкция

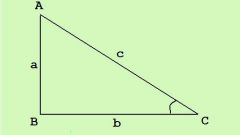
1. Если длины одного из катетов (a) и гипотенузы (с) прямоугольного треугольника известны, используйте для вычисления длины третьей стороны (b) теорему Пифагора. Из нее следует, что искомая величина должна быть равна квадратному корню из разности между возведенной в квадрат длиной гипотенузы и квадратом длины известного катета: b = √(c²-a²).
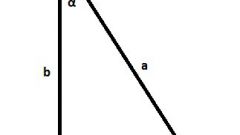
2. Зная величину угла (α) при вершине треугольника, лежащей напротив катета известной длины (a), тоже можно рассчитать неизвестную длину второго катета (b). Для этого примените определение одной из тригонометрических функций - тангенса - для острого угла. Из него вытекает, что искомая длина катета должна быть равна размеру известной стороны, поделенному на тангенс противолежащего угла: b = a/tg(α).
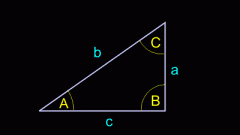
3. Определение котангенса для острого угла используйте для нахождения длины катета (b) в том случае, если в условиях приведена величина угла (β), примыкающего к другому катету известной длины (a). Формула в общем виде будет выглядеть почти так же, как и в предыдущем шаге, замените в ней лишь название функции и обозначение угла: b = a/ctg(β).
4. При известной длине гипотенузы (c) в вычислениях размеров катета (b) можно использовать определения основных тригонометрических функций - синуса и косинуса - для острых углов. Если в условиях дана величина угла (α) между этими двумя сторонами, из двух функций следует выбрать косинус. Умножьте длину гипотенузы на косинус известного угла: b = c*cos(α).
5. Определение синуса для острых углов используйте в тех случаях, когда кроме длины гипотенузы (c) дана величина угла (β) в вершине, лежащей напротив искомого катета (b). Формула расчета в общем виде будет схожа с предыдущей - она должна содержать произведение длины гипотенузы на синус угла заданной величины: b = c*sin(β).