Инструкция
1
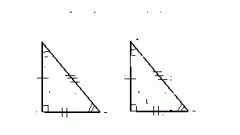
Проверьте, являются ли треугольники подобными по первому признаку. Данный признак показывает, что треугольники подобны в том случае, если два угла одного многоугольника равны двум углам другого. Доказательство данного правила выходит из второй теоремы равенства треугольников. Для определения этого необходимо воспользоваться транспортиром. Приложите его центральную часть к точке угла так, чтобы нижняя часть была параллельна или совпадала с одной из сторон фигуры. Угол равен тому значению, на которое указывает вторая сторона. Таким образом измерьте четыре угла и сравните.
2
Рассчитайте соотношение двух сторон одного треугольника к соответствующим сторонам другого. Если значения пропорции оказались равны и углы между сторонами одинаковы, то треугольники считаются подобными. Так гласит второй признак подобия. Для доказательства данного правила необходимо принять значение «к», которое равно отношению сходных сторон треугольника АВС и А1В1С1.
3
При помощи гомотетии с любым центром необходимо построить третий треугольник А2В2С2, две стороны которого будут равны сторонам первого треугольника умноженные на «к» и угол между ними будет соблюден. Если А1В1С1 и А2С2В2 будут равны по первому признаку равенства треугольников, то изначальные фигуры считаются подобными.
4
Определите соотношение всех сторон одного треугольника к соответствующим сторонам другого. При этом нет необходимости в измерении углов. Если пропорции оказались равными, то треугольники являются подобными по третьему признаку. Данная теорема имеет аналогичное доказательство, что и второй признак подобия. При этом третья фигура строится по всем трем сторонам.
5
Найдите коэффициент подобия для двух треугольников. Он равен отношению сходственных сторон подобных треугольников.
Видео по теме