Инструкция
1
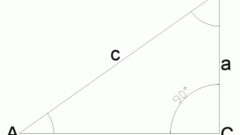
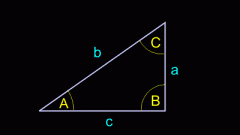
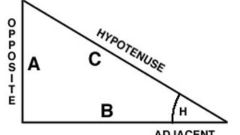
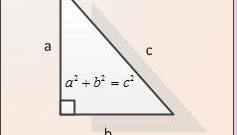
Классическая школьная формулировка теоремы Пифагора звучит так: квадрат гипотенузы равен сумме квадратов катетов. Таким образом, чтобы найти гипотенузу прямоугольного треугольника по двум катетам, надо поочередно возвести в квадрат длины катетов, сложить их и извлечь квадратный корень из результата. В изначальной своей формулировке теорема утверждала, что площадь квадрата, построенного на гипотенузе, равна сумме площадей двух квадратов, построенных на катетах. Однако современная алгебраическая формулировка не требует вводить понятие площади.
2
Пусть, например, дан прямоугольный треугольник, катеты которого равны 7 см и 8 см. Тогда, согласно теореме Пифагора, квадрат гипотенузы равен 7²+8²=49+64=113 см². Сама гипотенуза равна корню квадратному из числа 113. Получилось иррациональное число, которое идет в ответ.
3
Если катеты треугольника равны 3 и 4, тогда гипотенуза равна √25=5. При извлечении квадратного корня получилось натуральное число. Числа 3, 4, 5 составляют пифагорову тройку, потому что они удовлетворяют соотношению x²+y²=z², будучи все натуральными. Другие примеры пифагоровой тройки: 6, 8, 10; 5, 12, 13; 15, 20, 25; 9, 40, 41.
4
В том случае если катеты равны между собой, тогда теорема Пифагора переходит в более простое уравнение. Пусть, к примеру, оба катета равны числу A, а гипотенуза обозначена за C. Тогда C²=A²+A², C²=2A², C=A√2. В этом случае не нужно возводить в квадрат число A.
5
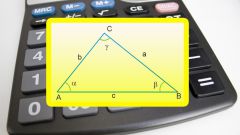
Теорема Пифагора – частный случай более общей теоремы косинусов, которая устанавливает соотношение между тремя сторонами треугольника для произвольного угла между какими-либо двумя из них.
Полезный совет
Прямоугольный треугольник, стороны которого соотносятся как 3:4:5, назван египетским треугольником, поскольку именно такие фигуры активно использовались архитекторами Древнего Египта. Он является также простейшим примером Героновых треугольников, в которых стороны и площадь представлены целыми числами.
Источники:
- как найти гипотенузу если катеты равны