Инструкция
1
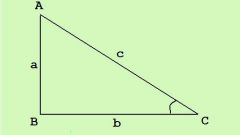
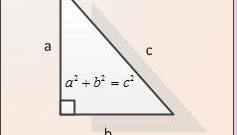
Теорему Пифагора используйте для нахождения длины гипотенузы (с) треугольника с известными величинами обоих катетов (a и b). Вам нужно возвести их размеры в квадрат и сложить, а из получившегося результата извлеките квадратный корень: c = √(a²+b²).
2
Если кроме размеров обоих катетов (a и b) в условиях дана высота (h), опущенная на гипотенузу (c), необходимость в вычислении степеней и корней отпадет. Перемножьте длины коротких сторон и разделите результат на высоту: c = a*b/h.
3
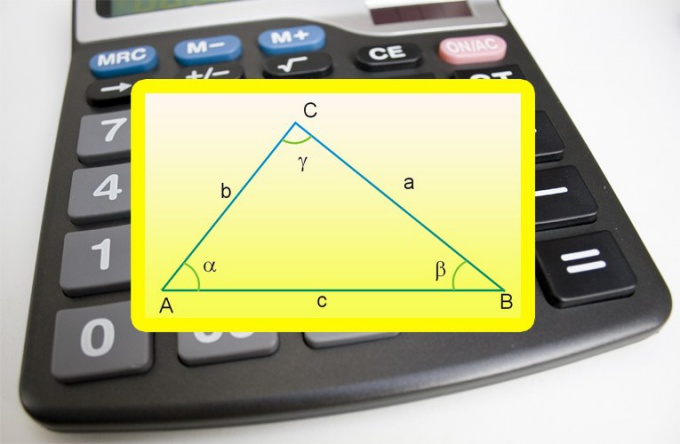
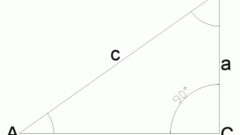
При известных величинах углов в вершинах прямоугольного треугольника, примыкающих к гипотенузе, и длине одного из катетов (a), воспользуйтесь определениями тригонометрических функций - синуса и косинуса. Выбор одной из них зависит от взаимного расположения известного катета и задействованного в расчетах угла. Если катет лежит напротив угла (α), исходите из определения синуса - длина гипотенузы (c) должна быть равна произведению длины этого катета на синус противолежащего угла: c = a*sin(α). Если же задействован угол (β), примыкающий к известному катету, используйте определение косинуса - умножайте длину стороны на косинус прилежащего к ней угла: c = a*cos(β).
4
Знание радиуса (R) описанной около прямоугольного треугольника окружности делает вычисление длины гипотенузы (c) очень простой задачей - просто увеличьте эту величину вдвое: c = 2*R.
5
Медиана по определению делит пополам сторону, на которую она опущена. Как следует из предыдущего шага, половина гипотенузы равна радиусу описанной окружности. Поскольку вершина, из которой на гипотенузу может быть опущена медиана, тоже обязана лежать на описанной окружности, длина этого отрезка равна радиусу. Значит, если длина медианы (f), опущенной из прямого угла, известна, для вычисления размера гипотенузы (c) можно использовать формулу, аналогичную предыдущей: c = 2*f.