Как вычислить длину гипотенузы

Гипотенуза – математический термин, встречающийся при рассмотрении прямоугольных треугольников. Это наибольшая из его сторон, противолежащая прямому углу. Вычислить длину гипотенузы можно разными способами, в том числе по теореме Пифагора.

Инструкция

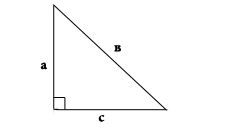
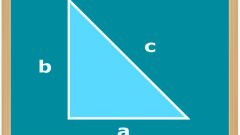
1. Треугольник является простейшей замкнутой геометрической фигурой, состоящей из трех вершин, углов и сторон, каждая из которых имеет свое название. Гипотенуза и два катета – стороны прямоугольного треугольника, длины которых связаны между собой и с другими величинами различными формулами.
2. Наиболее часто для того, чтобы вычислить длину гипотенузы, задачу сводят к применению теоремы Пифагора, которая звучит так: квадрат гипотенузы равен сумме квадратов катетов. Следовательно, ее длина находится вычислением квадратного корня из этой суммы.
3. Если известен только один катет и величина одного из двух углов, не являющихся прямыми, то можно воспользоваться тригонометрическими формулами. Предположим, дан треугольник ABC, в котором AC=c – гипотенуза, AB=a и BC=b – катеты, α – угол между a и c, β – угол между b и c. Тогда:c = a/cosα = a/sinβ = b/cosβ = b/sinα.
4. Решите задачу: найти длину гипотенузы, если известно, что AB=3 и угол BAC при этой стороне равен 30°.РешениеИспользуйте тригонометрическую формулу:AC = AB/cos30° = 3•2/√3 = 2•√3.
5. Это был простой пример на нахождение наибольшей стороны прямоугольного треугольника. Решите следующую: определить длину гипотенузы, если высота BH, проведенная к ней из противоположной вершины, равна 4. Известно также, что высота делит сторону на отрезки AH и HC, причем AH=3.
6. РешениеОбозначьте неизвестную часть гипотенузы HC=x. Как только вы найдете х, то сможете вычислить и длину гипотенузы. Итак, AC=x+3.
7. Рассмотрите треугольник AHB - он прямоугольный по определению высоты. Вы знаете длины двух его катетов, значит, можете найти гипотенузу a, которая является катетом треугольника ABC:a=√(AH² + BH²) = √(16+9) = 5.
8. Перейдите к другому прямоугольному треугольнику BHC и найдите его гипотенузу, которая равна b, т.е. второму катету треугольника ABC:b² = 16 + x².
9. Вернитесь к треугольнику ABC и запишите формулу Пифагора, составьте уравнение относительно х:(x+3)² = 25 + (16 + x²)x² + 6•x + 9 = 41 + x² → 6•x = 32 → x=16/3.
10. Подставьте х и найдите гипотенузу:AC = 16/3 + 3 = 25/3.