Чтобы сформулировать определение тангенса угла и других тригонометрических функций, рассматривают соотношение углов и сторон в прямоугольном треугольнике.
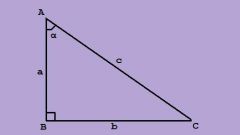
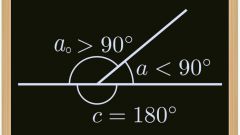
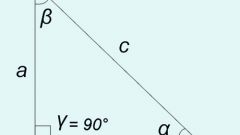
Известно, что сумма углов любого треугольника равна 180°. Следовательно, в прямоугольном сумма двух непрямых углов равна 90°. Стороны, образующие прямой угол, называются катетами. Третья сторона фигуры — гипотенуза. Каждый из двух острых углов прямоугольного треугольника образован гипотенузой и одним катетом, который называется «прилежащим» для этого угла. Соответственно, другой катет называется «противолежащим».
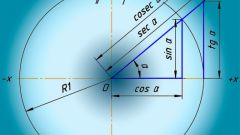
Тангесом угла называется отношение противолежащего катета к прилежащему. Попутно легко запомнить, что обратное отношение называется котангенсом угла. Тогда тангенс одного острого угла прямоугольного треугольника равен котангенсу второго. Также очевидно, что тангенс угла равен отношению синуса этого угла к его косинусу.
Отношение сторон — величина, не имеющая размерности. Тангенс, как синус, косинус и котангенс - это число. Каждому углу соответствует единственное значение тангенса (синуса, косинуса, котангенса). Значения тригонометрических функций для любого угла можно найти в математических таблицах Брадиса.
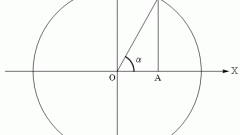
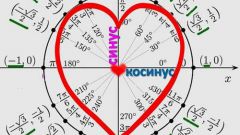
Чтобы узнать, какие значения может принимать тангенс угла, начертите единичную окружность. При изменении угла от 0° до 90° тангенс изменяется от нуля и устремляется в бесконечность. Изменение функции нелинейное, на графике легко найти промежуточные точки для построения кривой: tg 45°=1, tg30°= 1/√3, tg60°=√3.
Для отрицательных углов тангенс от нуля устремляется в минус бесконечность. Тангенс — периодическая функция с разрывами при приближении значения аргумента (угла) к 90° и -90°.
Видео по теме