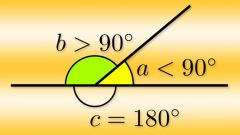Как найти тангенс внешнего угла

Если продолжить любую сторону многоугольника, в точке примыкания к ней смежной стороны получится развернутый угол, разделенный примыкающей стороной на два - внешний и внутренний. Внешним называется тот из них, который лежит вне периметра геометрической фигуры. Его величина связана с размерами внутреннего определенным соотношением, а величина внутреннего, в свою очередь, связана с другими параметрами многоугольника. Такая взаимосвязь позволяет, в частности, рассчитать по параметрам многоугольника тангенс внешнего угла.

Инструкция

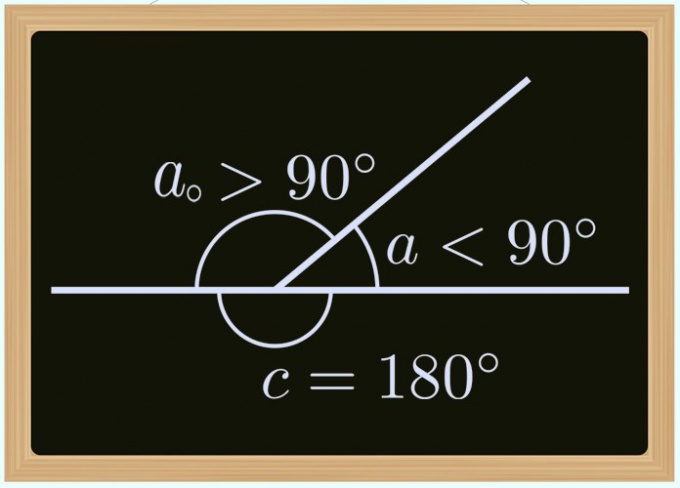
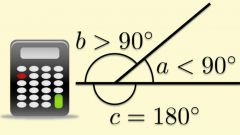
1. Если вам известна величина соответствующего внешнему углу (α₀) внутреннего (α), исходите из того, что вместе они всегда образуют развернутый угол. Величина развернутого равна 180° в градусах, что соответствует числу Пи в радианах. Из этого вытекает, что тангенс внешнего угла равен тангенсу разницы между 180° и величиной внутреннего угла: tg(α₀) = tg(180°-α₀). В радианах эту формулу надо записать так: tg(α₀) = tg(π-α₀).
2. Если в условиях задачи дана величина тангенса внутреннего угла (α), тангенс внешнего (α₀) приравнивайте к ней, но с измененным знаком: tg(α₀) = -tg(α).
3. Зная величину какой-нибудь другой тригонометрической функции, выражающей внутренний угол (α), проще всего для расчета тангенса внешнего (α₀) использовать обратную функцию, чтобы вычислить градусную меру внутреннего. Например, если известно значение косинуса, величину угла можно найти с использованием арккосинуса: α = arccos(cos(α)). Подставьте полученную величину в формулу из предыдущего шага: tg(α₀) = -tg(arccos(cos(α))).
4. В треугольнике величина любого внешнего угла (α₀) равна сумме величин двух внутренних углов (β и γ), лежащих в других вершинах фигуры. Если эти две величины известны, вычислите тангенс их суммы: tg(α₀) = tg(β+γ).
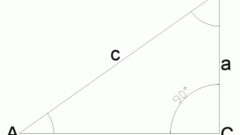
5. В прямоугольном треугольнике величину тангенса внешнего угла (α₀) можно рассчитать по длинам двух катетов. Разделите длину того из них, который лежит напротив вершины внешнего угла (a), на длину прилегающего к этой вершине (b). Результат надо брать с противоположным знаком: tg(α₀) = -a/b.
6. Если требуется вычислить тангенс внешнего угла (α₀) правильного многоугольника, вполне достаточно будет знания числа вершин (n) этой фигуры. По определению любой правильный многоугольник можно вписать в окружность, а любой внешний угол будет равен центральному углу круга, соответствующему длине стороны. Поскольку все стороны одинаковы, центральный угол можно рассчитать делением полного оборота - 360° - на количество сторон 360°/n. Значит, для получения искомого значения найдите тангенс от соотношения 360° и числа вершин: tg(α₀) = tg(360°/n).