Инструкция
1
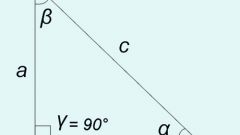
Используйте тригонометрические функции, если в условиях задачи даны лишь размеры сторон треугольника. Например, по длинам двух катетов (коротких сторон, прилегающих к прямому углу) можно вычислить любой из двух острых углов. Тангенс того угла (β), который прилегает к катету А, можно найти делением длины противолежащей ему стороны (катета В) на длину стороны А: tg(β) = В/А. А зная тангенс, можно вычислить и соответствующую ему величину угла в градусах. Для этого предназначена функция арктангенс: β = arctg(tg(β)) = arctg(В/А).
2
По этой же формуле можно найти величину и другого острого угла, лежащего напротив катета А. Просто поменяйте обозначения сторон. Но можно сделать это и иначе, с помощью другой пары тригонометрических функций - котангенса и арккотангенса. Котангенс угла b определяется делением длины прилежащего катета А на длину противолежащего В: tg(β) = А/В. А арккотангенс поможет извлечь из полученного значения величины угла в градусах: β = arсctg(сtg(β)) = arсctg(А/В).
3
Если в исходных условиях дана длина одного из катетов (А) и гипотенузы (С), то для вычисления углов используйте функции, обратные синусу и косинусу - арксинус и арккосинус. Синус острого угла β равен отношению длины лежащего напротив него катета В к длине гипотенузы С: sin(β) = В/С. Значит, для вычисления величины этого угла в градусах применяйте такую формулу: β = arcsin(В/С).
4
А значение косинуса угла β определяется отношением длины примыкающего к этой вершине треугольника катета А к длине гипотенузы С. Это значит, что для вычисления величины угла в градусах, по аналогии с предыдущей формулой, надо использовать такое равенство: β = arccos(А/С).
5
Теорема о сумме углов треугольника делает ненужным использование тригонометрических функций, если в условиях задачи дана величина одного из острых углов. В этом случае для вычисления неизвестного угла (α) просто отнимите от 180° величины двух известных углов - прямого (90°) и острого (β): α = 180° - 90° - β = 90° - β.