Как найти угол у треугольника, если известны две стороны?

В прямоугольном треугольнике можно достаточно просто найти угол, если известны две его стороны. Один из углов равен 90 градусов, два других являются всегда острыми. Вот эти углы и нужно будет найти. Для того, чтобы найти острый угол в прямоугольном треугольнике, необходимо знать значения всех трех его сторон. В зависимости от того, какие стороны вам известны, синусы острых углов можно найти, используя формулы для тригонометрических функций. Для отыскания значения угла по синусу используются четырехзначные математические таблицы.

Вам понадобится

• - Теорема Пифагора;
• - тригонометрическая функция sin;
• - четырехзначные математические таблицы Брадиса.

Инструкция

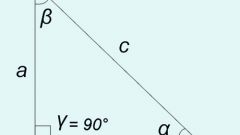
1. Используйте следующие обозначения для удобства составления формул, необходимых для расчетов: c – гипотенуза прямоугольного треугольника; a, b - катеты, которые образуют прямой угол; A – острый угол, находящийся напротив катета b; B - острый угол, находящийся напротив катета a.
2. Вычислите, чему равна длина неизвестной стороны треугольника. Примените для вычислений теорему Пифагора. Вычислите катет a, если известны значения гипотенузы c и катета b. Для этого вычтите из квадрата гипотенузы c квадрат катета b, а затем вычислите квадратный корень из полученного результата.
3. Вычислите катет b, если известны значения гипотенузы c и катета a. Для этого вычтите из квадрата гипотенузы c квадрат катета a, а затем вычислите квадратный корень из полученного результата.
4. Вычислите значение гипотенузы c, если известны два катета. Для этого получите сумму квадратов катетов a и b, а затем вычислите квадратный корень из полученного результата и при необходимости округлите до четырех знаков после запятой.
5. Вычислите синус угла A по формуле sinA = a/c. Используйте для вычислений калькулятор. Округлите при необходимости значение синуса угла A до четырех знаков после запятой.
6. Вычислите синус угла B по формуле sinB = b/c. Используйте для вычислений калькулятор. Округлите при необходимости значение синуса угла B до четырех знаков после запятой.
7. Найдите углы A и B по значениям их синусов. Используйте для определения значений углов таблицу VIII из четырехзначных математических таблиц Брадиса. Найдите в данной таблице значения синусов. Передвигайтесь от найденного значения влево и из первого столбца «А» возьмите градусы. Передвигайтесь от найденного значения вверх и из верхней строки «А» возьмите минуты. Например, если sin(A) = 0,8949, то угол A равен 63 градуса 30 минут.