Инструкция
1
Для задания каждой из сторон необходимо знать ее длину и еще один определенный параметр, который будет задавать положение треугольника на плоскости. Для этого, как правило, используются направленные отрезки - векторы.
Надо отметить, что на плоскости может быть бесконечно много равных векторов. Главное, чтобы они обладали равной длиной, точнее модулем |a|, а также направлением, которое задается наклоном к какой-либо оси (в декартовых координатах это ось 0Х). Поэтому для удобства векторы принято задавать с помощью радиус-векторов r=а, начало которых расположено в точке начала координат.
Надо отметить, что на плоскости может быть бесконечно много равных векторов. Главное, чтобы они обладали равной длиной, точнее модулем |a|, а также направлением, которое задается наклоном к какой-либо оси (в декартовых координатах это ось 0Х). Поэтому для удобства векторы принято задавать с помощью радиус-векторов r=а, начало которых расположено в точке начала координат.
2
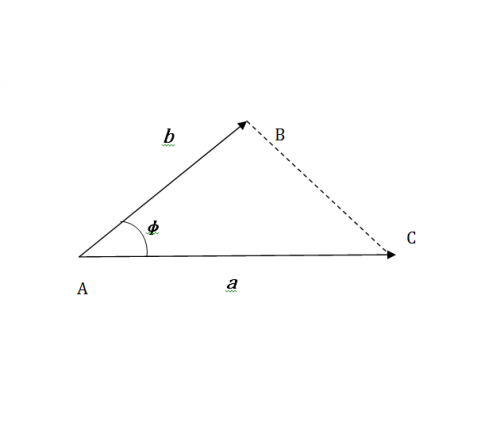
Для решения поставленного вопроса, необходимо определить скалярное произведение векторов а и b (обозначается (a,b)). Если угол между векторами ф, то, по определению, скалярное произведение двух ветров – это число, равное произведению модулей:
(a, b) = |a||b|cos ф (см. рис1).
В декартовых координатах, если а={x1, y1} и b={x2, y2}, то (a, b) = x1у2 +х2y1. При этом скалярный квадрат вектора (а,а)=|a|^2=x1^2 + x2^2. Для вектора b – аналогично. Итак, |a||b|cos ф = x1у2 +х2y1. Следовательно, cos ф=(x1у2 +х2y1)/(|a||b|). Данная формула является алгоритмом решения поставленной задачи в «плоском случае».
(a, b) = |a||b|cos ф (см. рис1).
В декартовых координатах, если а={x1, y1} и b={x2, y2}, то (a, b) = x1у2 +х2y1. При этом скалярный квадрат вектора (а,а)=|a|^2=x1^2 + x2^2. Для вектора b – аналогично. Итак, |a||b|cos ф = x1у2 +х2y1. Следовательно, cos ф=(x1у2 +х2y1)/(|a||b|). Данная формула является алгоритмом решения поставленной задачи в «плоском случае».
3
Пример1. Найти угол между сторонами треугольника, заданными векторами a={3, 5} и b ={-1, 4}.
Исходя из теоретических выкладок, приведенных выше, можно вычислить требуемый угол. cos ф=(x1y2 +x2y1)/(|a||b|)=(-3+20)/(9+25)^1/2(1+16)^1/2=18/6(17)^1/2=6/sqrt(17)=1,4552
Ответ: ф =arccos(1,4552).
Исходя из теоретических выкладок, приведенных выше, можно вычислить требуемый угол. cos ф=(x1y2 +x2y1)/(|a||b|)=(-3+20)/(9+25)^1/2(1+16)^1/2=18/6(17)^1/2=6/sqrt(17)=1,4552
Ответ: ф =arccos(1,4552).
4
Теперь следует рассмотреть случай объемной фигуры (многогранника). В данном варианте решения задачи угол меду сторонами воспринимается, как угол между ребрами боковой грани фигуры. Однако, строго говоря, основание так же является гранью многогранника. Тогда решение поставленной задачи сводится к рассмотрению первого «плоского случая». Но векторы будут задаваться уже тремя координатами.
Часто без внимания остается вариант задачи, когда стороны вообще не пересекаются, то есть лежат на скрещивающихся прямых. В данном случае понятие угла между ними также определено. При векторном задании отрезков прямых, способ определения угла меду ними един - скалярное произведение.
Часто без внимания остается вариант задачи, когда стороны вообще не пересекаются, то есть лежат на скрещивающихся прямых. В данном случае понятие угла между ними также определено. При векторном задании отрезков прямых, способ определения угла меду ними един - скалярное произведение.
5
Пример 2. Найти угол ф между сторонами произвольного многогранника, заданными векторами a={3, -5, -2} и b ={3, -4, 6}. Как только что выяснено, тот угол определятся его косинусом, причем
cos ф=(x1х2 +у1y2+z1z2)/(|a||b|)=(9+20-12)/(3^2+5^2+2^2)^1/2(3^2+4^2+6^2)^1/2=7/sqrt(29)•sqrt(61)=7/sqrt(1769)=0,1664
Ответ: ф=arccos(0,1664)
cos ф=(x1х2 +у1y2+z1z2)/(|a||b|)=(9+20-12)/(3^2+5^2+2^2)^1/2(3^2+4^2+6^2)^1/2=7/sqrt(29)•sqrt(61)=7/sqrt(1769)=0,1664
Ответ: ф=arccos(0,1664)
Видео по теме