Вам понадобится
- Таблица синусов и косинусов, таблица Брадиса
Инструкция
1
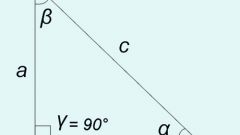
Обозначим углы треугольника буквами A, B и C, как это показано на рисунке. Угол BAC равен 90º, два других угла обозначим буквами α и β. Катеты треугольника обозначим буквами a и b, а гипотенузу буквой c.
2
3
Найдя один из углов, можно вспомнить, что сумма внутренних углов треугольника равна 180º. Значит, сумма α и β равна 180º - 90º = 90º.
Тогда, вычислив значение для α по таблицам, можем для нахождения β воспользоваться следующей формулой: β = 90º - α
Тогда, вычислив значение для α по таблицам, можем для нахождения β воспользоваться следующей формулой: β = 90º - α
4
Если неизвестна одна из сторон треугольника, то применяем теорему Пифагора: a²+b²=c². Выведем из нее выражение для неизвестной стороны через две другие и подставим в формулу для нахождения синуса или косинуса одного из углов.
Обратите внимание
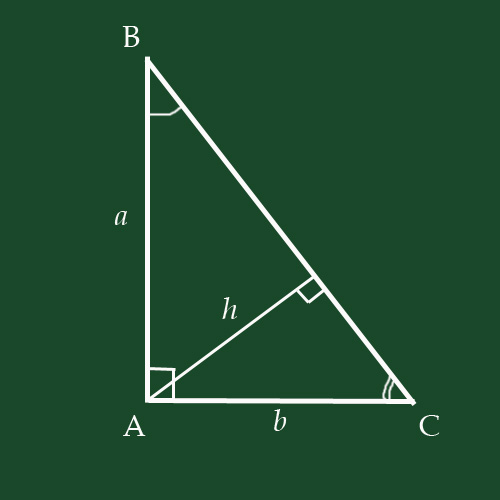
Высота h делит треугольник ABC на два прямоугольных треугольника, подобных ему. Здесь срабатывает признак подобия треугольников по трем углам.
Источники:
- Тригонометрия в прямоугольном треугольнике
- в прямоугольном треугольнике градусные меры внешних углов