Инструкция
1
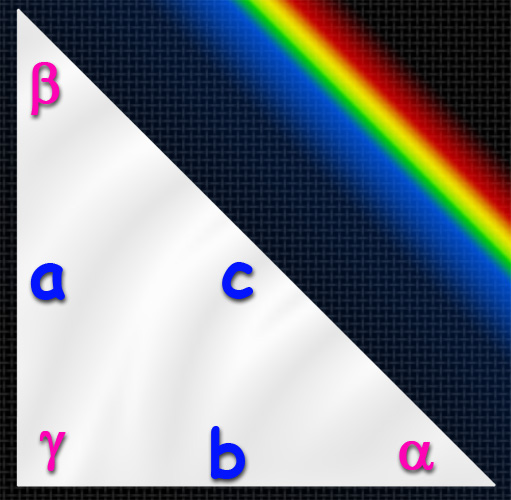
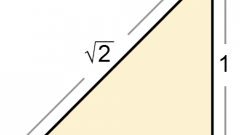
Используйте для вычисления величин углов (α, β, γ) определения тригонометрических функций через прямоугольный треугольник. Такое определение, например, для синуса острого угла формулируется как отношение длины противолежащего катета к длине гипотенузы. Значит, если известны длины катетов (A и B) и гипотенузы (C), то найти, например, синус угла α, лежащего напротив катета A можно, разделив длину стороны А на длину стороны C (гипотенузы): sin(α)=A/C. Узнав значение синуса этого угла можно найти его величину в градусах, использовав обратную синусу функцию - арксинус. То есть α=arcsin(sin(α))=arcsin(A/C). Таким же способом можно найти и величину другого острого угла в треугольнике, но в этом нет необходимости. Так как сумма всех углов треугольника всегда составляет 180°, а в прямоугольном треугольнике один из углов равен 90°, то величину третьего угла можно посчитать как разность между 90° и величиной найденного угла: β=180°-90°-α=90°-α.
2
Вместо определения синуса можно использовать определение косинуса острого угла, которое формулируется как отношение длины прилежащего к искомому углу катета к длине гипотенузы: cos(α)=B/C. И здесь задействуйте обратную тригонометрическую функцию (арккосинус), чтобы найти величину угла в градусах: α=arccos(cos(α))=arccos(B/C). После этого, как и в предыдущем шаге, останется найти величину недостающего угла: β=90°-α.
3
Можно воспользоваться аналогичным определением тангенса - он выражается соотношением длины противолежащего искомому углу катета к длине катета прилежащего: tg(α)=A/B. Величину угла в градусах снова определяйте через обратную тригонометрическую функцию - арктангенс: α=arctg(tg(α))=arctg(A/B). Формула величины недостающего угла останется без изменений: β=90°-α.
Видео по теме