Инструкция
1
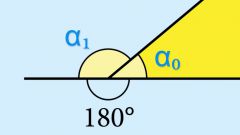
Из названия очевидно, что внешний угол лежит за пределами треугольника. Чтобы представить себе внешний угол, продлите сторону фигуры за вершину. Угол между продолжением стороны и второй стороной треугольника, выходящей из этой вершины, и будет внешним для угла треугольника при данной вершине.
2
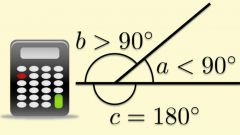
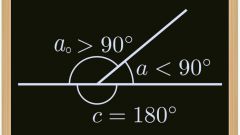
Очевидно, что острому углу треугольника соответствует тупой внешний угол. Для тупого угла внешний угол — острый, а внешний угол прямого угла — прямой. Два угла с общей стороной и сторонами, принадлежащими одной прямой, являются смежными и в сумме составляют 180°. Если угол треугольника α известен по условию, то смежный с ним внешний угол β определяется так:
β=180°-α.
3
Если угол α не задан, но известны другие два угла треугольника, то их сумма равна величине угла, внешнего по отношению к углу α. Это утверждение следует из того, что сумма всех углов треугольника равна 180°. В треугольнике внешний угол больше внутреннего угла, не смежного с ним.
4
Если градусная мера угла треугольника не задана, но из соотношения сторон известны тригонометрические зависимости, то по этим данным также можно найти внешний угол:
Sinα = Sin (180°-α)
Cosα = -Cos (180°-α)
tgα =- tg (180°-α).
5
Внешний угол треугольника можно определить, если не задан ни один внутренний угол, а известны только стороны фигуры. Из связей между элементами треугольника определите одну из тригонометрических функций внутреннего угла. Вычислите соответствующую функцию искомого внешнего угла и по тригонометрическим таблицам Брадиса найдите его величину в градусах.

Например, из формулы площади S=(b*c*Sinα)/2 определите Sinα, а затем внутренний и внешний угол в градусной мере. Или определите Cosα из теоремы косинусов a²=b²+c²-2bc*Cosα.