Как определить градус угла

Необходимость в вычислении величин углов в градусах возникает не только при решении различных задач из школьных учебников. Несмотря на то, что большинству из нас вся эта школьная тригонометрия кажется совершенно оторванной от жизни абстракцией, иногда вдруг выясняется, что под рукой нет других способов решения чисто практической задачи кроме школьных формул. К измерению в градусах величин углов это применимо в полной мере.

Инструкция

1. Если есть возможность воспользоваться соответствующим измерительным прибором, то выберите тот, который в наибольшей мере соответствует поставленной задаче. Например, для определения величины угла, начерченного на бумаге или другом аналогичном материале, вполне подойдет транспортир, а для определения угловых направлений на местности придется искать геодезический теодолит. Для измерений величин углов между сопрягающимися плоскостями каких-либо объемных предметов или агрегатов используйте угломеры - их существует много типов, отличающихся устройством, методом измерений и точностью. Можно найти и более экзотические приборы измерения углов в градусах.
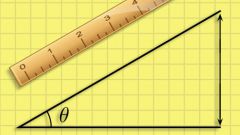
2. Если возможность измерений с помощью соответствующего инструмента отсутствует, то воспользуйтесь известными со школы тригонометрическими соотношениями между длинами сторон и величинами углов в треугольнике. Для этого будет достаточно возможности измерять не угловые, а линейные размеры - например, с помощью линейки, рулетки, метра, шагомера и т.д. С этого и начните - отмерьте от вершины угла вдоль двух его сторон удобное вам расстояние, запишите величины этих двух сторон треугольника, а затем измерьте и длину третьей стороны (расстояние между окончаниями этих сторон).
3. Выберите для вычисления величины угла в градусах одну из тригонометрических функций. Например, можно воспользоваться теоремой косинусов: квадрат длины стороны, лежащей напротив измеряемого угла, равен сумме квадратов двух других сторон, уменьшенной на удвоенное произведение длин этих сторон на косинус искомого угла (a² = b²+c²-2*b*c*cos(α)). Из этой теоремы выведите значение косинуса: cos(α) = (b²+c²-a²)/(2*b*c). Тригонометрическая функция, которая из косинуса восстанавливает величину угла в градусах, называется арккосинусом, а это значит, что формула в окончательном виде должна выглядеть так: α = arccos((b²+c²-a²)/(2*b*c)).
4. Подставьте измеренные размеры сторон треугольника в полученную на предыдущем шаге формулу и произведите вычисления. Это можно сделать с помощью любого калькулятора, включая и те, что предлагают различные онлайн-сервисы в интернете.