Как найти косинус альфа

Словом «косинус» называют одну из тригонометрических функций, которая при написании обозначается как cos. Наиболее часто иметь с ней дело приходится при решении задач на нахождение параметров правильных фигур в геометрии. В таких задачах величины углов в вершинах многоугольников обозначаются, как правило, прописными буквами греческого алфавита. Если речь при этом идет о прямоугольном треугольнике, то по одной этой букве иногда можно выяснить, который из углов имеется в виду.

Инструкция

1. Если величина угла, обозначенная буквой α, известна из условий задачи, то для нахождения значения, соответствующего косинусу альфа, можно воспользоваться стандартным калькулятором ОС Windows. Запускается он через главное меню операционной системы - нажмите кнопку Win, раскройте в меню раздел «Все программы», перейдите в подраздел «Стандартные», а затем в секцию «Служебные». Там и найдете строку «Калькулятор» - кликните ее для запуска приложения.
2. Нажмите сочетание клавиш Alt + 2, чтобы переключить интерфейс приложения в «инженерный» (в других версиях ОС - «научный») вариант. Затем введите величину угла α и щелкните указателем мыши кнопку, обозначенную буквами cos - калькулятор произведет вычисление функции и отобразит результат.
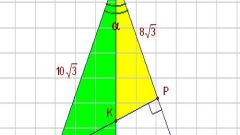
3. Если вычислить косинус угла α нужно в прямоугольном треугольнике, то, по-видимому, это один из двух острых углов. При правильном обозначении сторон такого треугольника гипотенузу (самую длинную сторону) обозначают буквой c, а лежащий напротив нее прямой угол - греческой буквой γ. Две другие стороны (катеты) обозначают буквами a и b, а лежащие напротив них острые углы - α и β. Для величин острых углов прямоугольного треугольника существуют соотношения, которые позволят вычислять косинус, даже не зная величины самого угла.
4. Если в прямоугольном треугольнике известны длины сторон b (катета, прилежащего к углу α) и c (гипотенузы), то для вычисления косинуса α поделите длину этого катета на длину гипотенузы: cos(α)=b/c.
5. В произвольном треугольнике значение косинуса угла α неизвестной величины можно вычислить, если в условиях даны длины всех сторон. Для этого сначала возведите в квадрат длины всех сторон, потом полученные значения для двух сторон, прилежащих к углу α сложите, а полученное значение для противолежащей стороны отнимите от результата. Затем полученную величину разделите на удвоенное произведение длин прилегающих к углу α сторон - это и будет искомый косинус угла α: cos(α)=(b²+c²-a²)/(2*b*c). Это решение вытекает из теоремы косинусов.