Инструкция
1
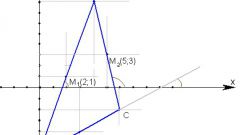
Перед тем, как начать процесс нахождения координат вершины, определитесь с исходными данными. Примите, что искомая вершина принадлежит треугольнику ABC, в котором известны координаты двух остальных вершин, а также числовые значения углов, равные «e» и «k» по стороне AB.
2
Совместите новую систему координат с одной из сторон треугольника AB таким образом, чтобы начало системы координат совпадало с точкой A, координаты которой вам известны. Вторая вершина B будет лежать на оси OX, и ее координаты вам также известны. Определите по оси ОХ значение длины стороны AB согласно координатам и примите ее равной «m».
3
Опустите перпендикуляр из неизвестной вершины C на ось ОХ и на сторону треугольника AB соответственно. Получившаяся высота «y» и определяет значение одной из координат вершины C по оси OY. Примите, что высота «y» делит сторону AB на два отрезка, равные «x» и «m – x».
4
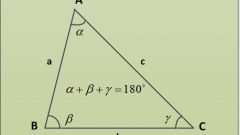
Поскольку вам известны значения всех углов треугольника, значит, известны и значения их тангенсов. Примите значения тангенсов для углов, примыкающих к стороне треугольника AB, равными tan(e) и tan(k).
5
Введите уравнения для двух прямых, проходящих по сторонам AC и BC соответственно: y = tan(e) * x и y = tan(k) * (m – x). Затем найдите пересечение этих прямых, используя преобразованные уравнения прямых: tan(e) = y/x и tan(k) = y/(m – x).
6
Если принять, что tan(e)/tan(k) равняется (y/x) /( y/ (m – x)) или после сокращения «y» - (m – x) / x , в результате вы получите искомые значения координат, равные x = m / (tan(e)/tan(k) + e) и y = x * tan(e).
7
Подставьте значения углов (e) и (k), а также найденное значение стороны AB = m в уравнения x = m / (tan(e)/tan(k) + e) и y = x * tan(e).
8
Преобразуйте новую систему координат в исходную систему координат, поскольку между ними установлено взаимно-однозначное соответствие, и получите искомые координаты вершины треугольника ABC.
Видео по теме