Инструкция
1
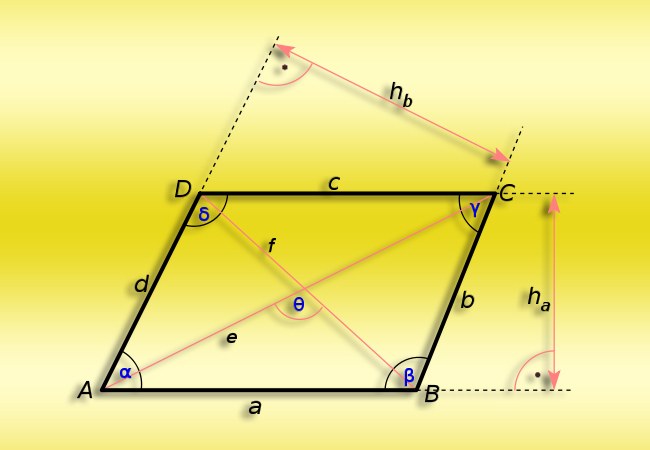
Если требуется вычислить величину острого (α) угла в параллелограмме, величина хотя бы одного из углов (β) которого известна, то исходите из того, что сумма всех четырех углов обязана быть равна 360°. Поскольку одно из основных свойств этой фигуры заключается в одинаковости противоположных вершин, то для вычисления величин углов в паре неизвестных сторон разделите пополам разность между 360° и удвоенной величиной известного угла: α=(360°-2*β)/2.
2
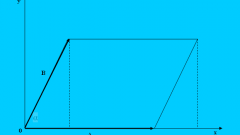
Если нужно определить величину острого угла (α) в параллелограмме, в котором известны длины смежных сторон (А и В) и меньшей из диагоналей (d), то рассмотрите треугольник, образованный этими тремя отрезками. Косинус нужного вам угла будет равен соотношению между суммой возведенных в квадрат длин сторон, из которых вычтена возведенная в квадрат длина диагонали, и удвоенным произведением этих же двух сторон - это вытекает из теоремы косинусов. Тригонометрическая функция, которая по значению косинуса угла восстанавливает его величину в градусах, называется арккосинусом. Ее и примените к соотношению, полученному с помощью теоремы косинусов: α=arccos((А²+В²-d²)/(2*А*В)).
3
Если, как и в предыдущем варианте, известны длины смежных сторон (А и В), а вместо короткой диагонали дана величина длинной (D), то алгоритм немного усложнится. Напротив длинной диагонали лежит тупой угол параллелограмма, поэтому сначала вычислите его величину по формуле из предыдущего шага, а затем примените формулу из первого шага. В общем виде формулу можно записать так: α=(360°-2*arccos((А²+В²-D²)/(2*А*В)))/2.
4
Если кроме длин смежных сторон параллелограмма (А и В) известна его площадь (S), то этого достаточно для вычисления величины острого угла (α). Синус этого угла рассчитайте из соотношения между площадью и произведением длин сторон, а затем примените к результату функцию арксинус - она работает аналогично арккосинусу: α=arcsin(S/(А*В)).
Видео по теме