Инструкция
1
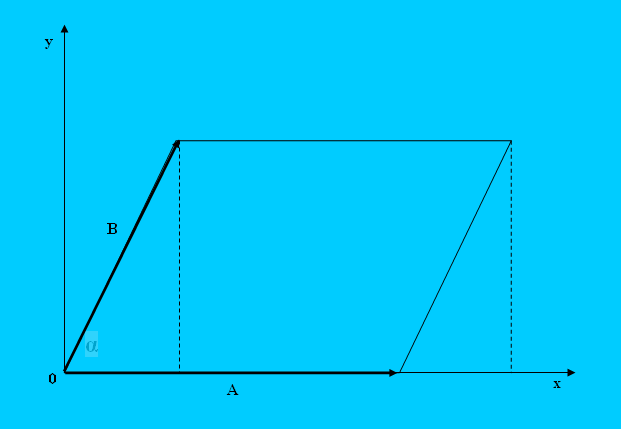
Найдите длины векторов, если заданы их координаты. Пусть, например, вектор A имеет координаты (a1,a2) на плоскости. Тогда длина вектора A равна |A|=√(a1²+a2²). Аналогично находится модуль вектора B: |B|=√(b1²+b2²), где b1 и b2 – координаты вектора B на плоскости.
2
Площадь параллелограмма находится по формуле S=|A|•|B|•sin(A^B), где A^B – угол между заданными векторами A и B. Синус можно найти через косинус, используя основное тригонометрическое тождество: sin²α+cos²α=1. Косинус же можно выразить через скалярное произведение векторов, записанное в координатах.
3
Скалярное произведение вектора A на вектор B обозначается как (A,B). По определению, оно равно (A,B)=|A|•|B|•cos(A^B). А в координатах скалярное произведение записывается так: (A,B)=a1•b1+a2•b2. Отсюда можно выразить косинус угла между векторами: cos(A^B)=(A,B)/|A|•|B|=(a1•b1+a2•b2)/√(a1²+a2²)•√(a2²+b2²). В числителе – скалярное произведение, в знаменателе – длины векторов.
4
Теперь можно выразить синус из основного тригонометрического тождества: sin²α=1-cos²α, sinα=±√(1-cos²α). Если предположить, что угол α между векторами – острый, «минус» при синусе можно отбросить, оставив только знак «плюс», поскольку синус острого угла может быть только положительным (или нулевым при нулевом угле, но здесь угол ненулевой, это отображается в условии неколлинеарности векторов).
5
Теперь надо подставить координатное выражение для косинуса в формулу синуса. После этого останется лишь записать результат в формулу площади параллелограмма. Если всё это проделать и упростить числовое выражение, то получится, что S=a1•b2-a2•b1. Таким образом, площадь параллелограмма, построенного на векторах A(a1,a2) и B(b1,b2), находится по формуле S=a1•b2-a2•b1.
6
Полученное выражение является детерминантом матрицы, составленной из координат векторов A и B:a1 a2b1 b2.
7
Действительно, чтобы получить определитель матрицы размерности два, нужно перемножить элементы главной диагонали (a1,b2) и вычесть из этого произведение элементов побочной диагонали (a2,b1).
Видео по теме