Как решать вектор

В линейной алгебре и в геометрии понятие вектор определяется по разному. В алгебре вектором называется элемент векторного пространства. В геометрии же вектором называют упорядоченную пару точек евклидового пространства - направленный отрезок. Над векторами определены линейные операции – сложение векторов и умножение вектора на некоторое число.

Инструкция

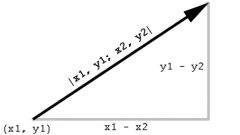
1. Правило треугольника.
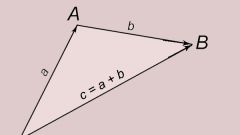
   Суммой двух векторов a и o называется вектор, начало которого совпадает с началом вектора a, а конец лежит на конце вектора o, при этом начало вектора o совпадает с концом вектора a. Построение этой суммы представлено на рисунке.
   
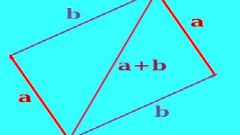
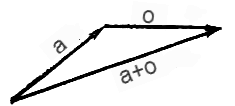
2. Правило параллелограмма.
   Пусть векторы a и o имеют общее начало. Достроим эти векторы до параллелограмма. Тогда сумма векторов a и o совпадает с диагональю параллелограмма, исходящей из начала векторов a и o.
   
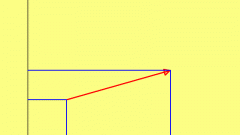
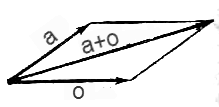
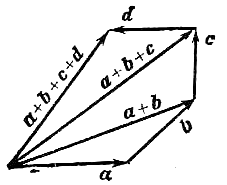
3. Сумму большего количества векторов можно найти, последовательно применяя к ним правило треугольника. На рисунке представлена сумма четырёх векторов.
   
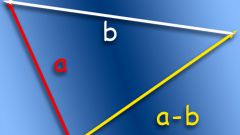
4. Произведением вектора a на число ? называется число ?a такое, что |?a| = |?| * |a|. Полученный при умножении на число вектор параллелен исходному вектору или лежит с ним на одной прямой. Если ?>0, то векторы a и ?a являются однонаправленными, если ?<0, то векторы a и ?a направлены в разные стороны.