Вам понадобится
  • - определение вектора;
  • - свойства векторов;
  • - калькулятор;
  • - таблица Брадиса или ПК.
Инструкция
1
Вычислить вектор, можно зная его координаты. Для этого определите координаты начала и конца вектора. Пусть они будут равны (x1;y1) и (x2;y2). Чтобы произвести вычисление вектора, найдите его координаты. Для этого от координат конца вектора отнимите координаты его начала. Они будут равны (x2- x1;y2-y1). Примите x= x2- x1; y= y2-y1, тогда координаты вектора будут равны (x;y).
2
Определите длину вектора. Это можно сделать просто, измерив ее линейкой. Но если известны координаты вектора, рассчитайте длину. Для этого найдите сумму квадратов координат вектора и извлеките из получившегося числа корень квадратный. Тогда длина вектора будет равна d=√(x²+y²).
3
После этого найдите направление вектора. Для этого определите угол α между ним и осью ОХ. Тангенс этого угла равен отношению координаты y вектора к координате x (tg α= y/x). Чтобы найти угол, воспользуйтесь в калькуляторе функцией арктангенса, таблицей Брадиса или ПК. Зная длину вектора и его направление относительно оси, можно найти положение в пространстве любого вектора.
4
Пример:

координаты начала вектора равны (-3;5), а координаты конца (1;7). Найдите координаты вектора (1-(-3);7-5)=(4;2). Тогда его длина составит d=√(4²+2²)=√20≈4,47 линейных единиц. Тангенс угла между вектором и осью ОХ составит tg α=2/4=0,5. Арктангенс этого угла округленно равен 26,6º.
5
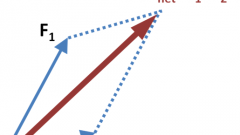
Найдите вектор, который представляет собой сумму двух векторов, координаты которых известны. Для этого сложите соответствующие координаты векторов, которые складываются. Если координаты векторов, которые складываются, равны соответственно(x1;y1) и (x2;y2), то их сумма будет равна вектору с координатами ((x1+x2;y1+y2)). Если нужно найти разность двух векторов, то находите сумму, предварительно умножив координаты вектора, который вычитается на -1.
6
Если известны длины векторов d1 и d2, и угол между ними α, найдите их сумму, используя теорему косинусов. Для этого найдите сумму квадратов длин векторов, а из получившегося числа вычтите удвоенное произведение этих длин, умноженное на косинус угла между ними. Из получившегося числа извлеките корень квадратный. Это и будет длина вектора, являющегося суммой двух данных векторов (d=√(d1²+d2²-d1∙d2∙Cos(α)).