Инструкция
1
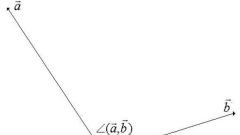
Определить угол между двумя прямыми в пространстве можно, даже если они не пересекаются. В этом случае нужно мысленно совместить начала их направляющих векторов и вычислить величину получившегося угла. Иными словами, это любой из смежных углов, образованных скрещивающимися прямыми, проведенными параллельно данным.
2
Существует несколько способов задания прямой в пространстве, например, векторно-параметрический, параметрический и канонический. Три упомянутых метода удобно использовать при нахождении угла, т.к. все они предполагают введение координат направляющих векторов. Зная эти величины, можно определить образованный угол по теореме косинусов из векторной алгебры.
3
Предположим, две прямые L1 и L2 заданы каноническими уравнениями:L1: (x – x1)/k1 = (y – y1)/l1 = (z – z1)/n1;L2: (x – x2)/k2 = (y – y2)/l2 = (z – z2)/n2.
4
Используя величины ki, li и ni, запишите координаты направляющих векторов прямых. Назовите их N1 и N2:N1 = (k1, l1, n1);N2 = (k2, l2, n2).
5
Формула для косинуса угла между векторами представляет собой соотношение между их скалярным произведением и результатом арифметического умножения их длин (модулей).
6
Определите скалярное произведение векторов как сумму произведений их абсцисс, ординат и аппликат:N1•N2 = k1•k2 + l1•l2 + n1•n2.
7
Вычислите квадратные корни из сумм квадратов координат, чтобы определить модули направляющих векторов:|N1| = √(k1² + l1² + n1²);|N2| = √(k2² + l2² + n2²).
8
Используйте все полученные выражения, чтобы записать общую формулу косинуса угла N1N2:cos (N1N2) = (k1•k2 + l1•l2 + n1•n2)/( √(k1² + l1² + n1²)•√(k2² + l2² + n2²)).Чтобы найти величину самого угла, посчитайте arccos от этого выражения.
9
Пример: определить угол между заданными прямыми:L1: (x - 4)/1 = (y + 1)/(-4) = z/1;L2: x/2 = (y - 3)/(-2) = (z + 4)/(-1).
10
Решение:N1 = (1, -4, 1); N2 = (2, -2, -1).N1•N2 = 2 + 8 – 1 = 9;|N1|•|N2| = 9•√2.cos (N1N2) = 1/√2 → N1N2 = π/4.