Инструкция
1
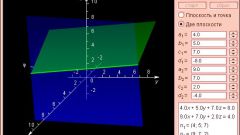
Плоскость – это основная пространственная фигура геометрии, которая участвует в построении всех двухмерных и трехмерных форм, таких как треугольник, квадрат, параллелепипед, призма, окружность, эллипс и т.д. В каждом конкретном случае она ограничивается определенным набором линий, которые, пересекаясь, образуют замкнутую фигуру.
2
В общем же виде плоскость не ограничивается ничем, она простирается по разные стороны от своей образующей прямой. Это плоская бесконечная фигура, которая, тем не менее, может быть задана уравнением, т.е. конечными числами, которые являются координатами ее нормального вектора.
3
Исходя из вышесказанного, можно найти угол между любым вектором и плоскостью, используя формулу косинуса угла между двумя векторами. Направленные отрезки могут быть расположены в пространстве как угодно, однако каждый вектор обладает таким свойством, что его можно перемещать без потери основных характеристик, направления и длины. Этим и нужно воспользоваться, чтобы рассчитать угол между отстоящими векторами, поместив их зрительно в одну начальную точку.
4
Итак, пусть задан вектор V = (а, b, с) и плоскость А•x + В•y + C•z = 0, где А, В и C – координаты нормали N. Тогда косинус угла α между векторами V и N равен:сos α = (а•А + b•В + с•C)/(√(а² + b² + с²)•√(А² + В² + C²)).
5
Чтобы вычислить величину угла в градусах или радианах, нужно от получившегося выражения рассчитать функцию, обратную к косинусу, т.е. арккосинус:α = аrссos ((а•А + b•В + с•C)/(√(а² + b² + с²)•√(А² + В² + C²))).
6
Пример: найдите угол между вектором (5, -3, 8) и плоскостью, заданной общим уравнением 2•x – 5•y + 3•z = 0.Решение: выпишите координаты нормального вектора плоскости N = (2, -5, 3). Подставьте все известные значения в приведенную формулу:сos α = (10 + 15 + 24)/√3724 ≈ 0,8 → α = 36,87°.
Видео по теме