Инструкция
1
Если прямая задана двумя точками, найдите ее уравнение по формуле (х-х1)/(х2-х1)=(у-у1)/(у2-у1)=(z-z1)/(z2-z1). Подставьте координаты первой точки (х1,у1,z1) и второй точки (х2,у2,z2) в уравнение и упростите выражение.
2
Возможно, точки вам заданы лишь двумя координатами, например, (х1, у1) и (х2,у2), в таком случае уравнение прямой найдите по упрощенной формуле (х-х1)/(х2-х1)=(у-у1)/(у2-у1). Чтобы сделать его более наглядным и удобным, выразите у через х – приведите уравнение к виду у=kх+b.
3
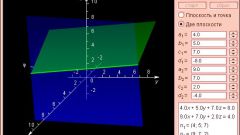
Для того чтобы найти уравнение прямой, являющейся линией пересечения двух плоскостей, составьте уравнения этих плоскостей в систему и решите ее. Как правило, плоскость задана выражением вида Ах+Ву+Сz+D=0. Таким образом, решая систему А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 относительно неизвестных х и у (то есть z вы берете как параметр или число), вы получите два приведенных уравнения: х=mz+a и y=nz+b.
4
Если есть необходимость, из приведенных уравнений получите каноническое уравнение прямой. Для этого выразите z из каждого уравнения и приравняйте полученные выражения: (х-а)/m=(y-b)/n=z/1. Вектор с координатами (m,n,1) будет направляющим вектором этой прямой.
5
Прямая может быть также задана точкой и коллинеарным (сонаправленным) ей вектором, в таком случае для поиска уравнения воспользуйтесь формулой (х-х1)/m=(y-y1)/n=(z-z1)/p, где (х1,у1,z1) – координаты точки, а (m,n,p) – коллинеарный вектор.
6
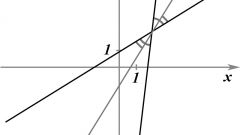
Для того чтобы определить уравнение прямой, заданной графически на плоскости, найдите точку ее пересечения с осями координат и подставьте в уравнение. В случае, если известен угол ее наклона к оси ох, вам достаточно будет найти тангенс этого угла (это будет коэффициент перед х в уравнении) и точку пересечения с осью оу (это будет свободный член уравнения).