Инструкция
1
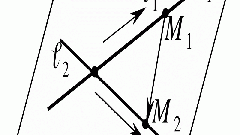
Рассмотрим определение точки пересечения прямой с плоскостью частного положения (рисунок 1).
Прямая l пересекает фронтально-проектирующую плоскость Σ. Точка их пересечения K принадлежит и прямой и плоскости, значит, фронтальная проекция K2 лежит на Σ2 и l2. То есть, K2= l2×Σ2, а ее горизонтальная проекция K1 определяется на l1 при помощи линии проекционной связи.
Таким образом, искомая точка пересечения K(K2K1) строится непосредственно без применения вспомогательных плоскостей.
Аналогично определяются точки пересечения прямой с любыми плоскостями частного положения.
2
Рассмотрим определение точки пересечения прямой с плоскостью общего положения. На рисунке 2 в пространстве заданы произвольно расположенные плоскость Θ и прямая l . Для определения точки пересечения прямой с плоскостью общего положения применяется метод вспомогательных секущих плоскостей в следующем порядке:
3
Через прямую l проводится вспомогательная секущая плоскость Σ.
Для упрощения построений это будет проектирующая плоскость.
4
Далее строится линия пересечения MN вспомогательной плоскости с заданной: MN=Σ×Θ.
5
Отмечается точка K пересечения прямой l и построенной линии пересечения MN. Она и является искомой точкой пересечения прямой и плоскости.
6
Применим это правило для решения конкретной задачи на комплексном чертеже.
Пример. Определить точку пересечения прямой l с плоскостью общего положения, заданной треугольником ABC (рисунок 3).
7
Через прямую l проводится вспомогательная секущая плоскость Σ, перпендикулярная плоскости проекции Π2. Ее проекция Σ2 совпадает с проекцией прямой l2.
8
Строится линия MN. Плоскость Σ пересекает AB в точке M. Отмечается ее фронтальная проекция M2= Σ2×A2B2 и горизонтальная M1 на A1B1 по линии проекционной связи.
Плоскость Σ пересекает сторону AC в точке N. Ее фронтальная проекция N2=Σ2×A2C2, горизонтальная проекция N1 на A1C1.
Прямая MN принадлежит одновременно обеим плоскостям, а, значит, является линией их пересечения.
9
Определяется точка K1 пересечения l1 и M1N1, затем с помощью линии связи строится точка K2. Итак, K1 и K2 – проекции искомой точки пересечения K прямой l и плоскости ∆ ABC:
K(K1K2)= l(l1l2)× ∆ ABC(A1B1C1, A2B2C2).
При помощи конкурирующих точек М,1 и 2,3 определяется видимость прямой l относительно данной плоскости ∆ ABC.